
题目列表(包括答案和解析)
| 19 |
| 36 |
| 1 |
| 2 |
| 1 |
| x |
下列四种说法:①命题“若![]() 或
或![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() 或
或![]() ,则
,则![]() ”;②四面体
”;②四面体![]() 的外接球球心在棱
的外接球球心在棱![]() 上,且
上,且![]() ,
,![]() ,则在外接球球面上
,则在外接球球面上![]() 、
、![]() 两点间的球面距离是
两点间的球面距离是![]() ;③若
;③若![]() ,则复数
,则复数![]() 在复平面内对应的点位于第三象限;④在某项测量中,测量结果
在复平面内对应的点位于第三象限;④在某项测量中,测量结果![]() 服从正态分布
服从正态分布![]() (
(![]() ).若
).若![]() 在
在![]() 内取值的概率为0.4,则
内取值的概率为0.4,则![]() 在
在![]() 内取值的概率为0.4;其中说法正确的有( )
内取值的概率为0.4;其中说法正确的有( )
A.4个 B.3个 C.2个 D.1个
 ;
; ,1)且与函数y=
,1)且与函数y=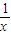 图象相切的直线方程是4x+y-3=0.
图象相切的直线方程是4x+y-3=0. ;
; ,1)且与函数y=
,1)且与函数y= 图象相切的直线方程是4x+y-3=0.
图象相切的直线方程是4x+y-3=0.| 19 |
| 36 |
| 1 |
| 2 |
| 1 |
| x |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com