为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：

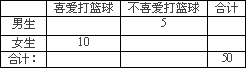
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为．

(1)请将上面的列联表补充完整；

(2)是否有99.5％的把握认为喜爱打篮球与性别有关？说明你的理由；

(3)已知喜爱打篮球的10位女生中，A₁，A₂，A₃还喜欢打羽毛球，B₁，B₂，B₃还喜欢打乒乓球，C₁，C₂还喜欢踢足球，现在从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查，求女生B₁和C₁不全被选中的概率．

下面的临界值表供参考：

(参考公式：，其中n＝a＋b＋c＋d．)