
题目列表(包括答案和解析)
(本小题满分10分)(注意:在试题卷上作答无效)
在△![]() 中,角
中,角![]() 、
、![]() 、
、![]() 所对的边分别为
所对的边分别为![]() 、
、![]() 、
、![]() ,且
,且![]() .
.
(Ⅰ)若![]() ,求角
,求角![]() ;
;
w ww.ks 5u.c om
(Ⅱ)设![]() ,
,![]() ,试求
,试求![]() 的最大值.
的最大值.
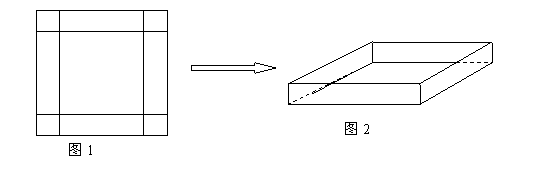
(本小题满分15分)在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由. W ww.k s 5u.c om


(本小题满分15分)在一次数学实践活动课上,老师给一个活动小组安排了这样的一个任务:设计一个方案,将一块边长为4米的正方形铁片,通过裁剪、拼接的方式,将它焊接成容积至少有5立方米的长方体无盖容器(只有一个下底面和侧面的长方体).该活动小组接到任务后,立刻设计了一个方案,如下图所示,按图1在正方形铁片的四角裁去四个相同的小正方形后,将剩下的部分焊接成长方体(如图2).请你分析一下他们的设计方案切去边长为多大的小正方形后能得到的最大容积,最大容积是多少?是否符合要求?若不符合,请你帮他们再设计一个能符合要求的方案,简单说明操作过程和理由. W ww.k s 5u.c om

(本小题满分15分)已知公差大于零的等差数列![]() 的前n项和为Sn,且满足:
的前n项和为Sn,且满足:![]() ,
,![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ;
;
(2)若数列![]() 是等差数列,且
是等差数列,且![]() ,求非零常数c;W ww.k s 5u.c om
,求非零常数c;W ww.k s 5u.c om
(3)若(2)中的![]() 的前n项和为
的前n项和为![]() ,求证:
,求证:![]()
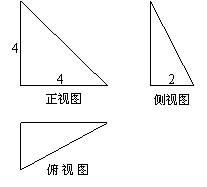
一个三棱w ww.ks 5u.c om锥的三视图是三个直角三角形,如图所示,在包围该三棱锥的外接球内任取一点,该点落在三棱锥内部的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 |
一、填空题
1.  ; 2.
; 2. ; 3.
; 3. ; 4.
; 4. ; 5.
; 5. ;
;
6. ;
7.
;
7. ; 8.3; 9.
; 8.3; 9. . 10.
. 10.
11. ; 12.
; 12. ; 13.
; 13. ; 14.
; 14. .
.
二、解答题
15.解:(1)由 得:
得:
 ,
,
由正弦定理知:  ,
,
(2) ,
,
由余弦定理知:
16.解:(Ⅰ)证明:取 的中点
的中点 ,连接
,连接
 因为
因为 是正三角形,
是正三角形,
所以
又 是正三棱柱,
是正三棱柱,
所以 面
面 ,所以
,所以
所以有 面
面
因为 面
面
所以 ;
;
(Ⅱ) 为
为 的三等分点,
的三等分点, .
.
连结 ,
, ,
,
∵  ,∴
,∴  .
.
∴  , ∴
, ∴ 
又∵ 面
面 ,
, 面
面
∴  平面
平面
17.解 (Ⅰ)设点P的坐标为(x,y),由P(x,y)在椭圆上,得


又由 知
知 ,
,
所以
(Ⅱ) 当 时,点(
时,点( ,0)和点(-
,0)和点(- ,0)在轨迹上.
,0)在轨迹上.
当 且
且 时,由
时,由 ,得
,得 .
.
又 ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF ,所以有
,所以有
综上所述,点T的轨迹C的方程是
(Ⅲ) C上存在点M( )使S=
)使S= 的充要条件是
的充要条件是
由③得 ,由④得
,由④得 所以,当
所以,当 时,存在点M,使S=
时,存在点M,使S= ;
;
当 时,不存在满足条件的点M.
时,不存在满足条件的点M.
当 时,
时, ,
,
由 ,
,
 ,
,
 ,得
,得
18.解:(1) (或
(或 )(
)( )
)
(2)
当且仅当 ,即V=
,即V=
所以,博物馆支付总费用的最小值为7500元.
(3)解法1:由题意得不等式:
当保护罩为正四棱锥形状时, ,代入整理得:
,代入整理得: ,解得
,解得 ;
;
当保护罩为正四棱柱形状时, ,代入整理得:
,代入整理得: ,解得
,解得
又底面正方形面积最小不得少于 ,所以,底面正方形的面积最小可取
,所以,底面正方形的面积最小可取
解法2. 解方程 ,即
,即 得两个根为
得两个根为
由于函数 在
在 上递减,在
上递减,在 上递增,所以当
上递增,所以当 时,总费用超过8000元,所以V取得最小值
时,总费用超过8000元,所以V取得最小值
由于保护罩的高固定为 .所以当保护罩为正四棱柱时,保护罩底面积最小,
.所以当保护罩为正四棱柱时,保护罩底面积最小, m2
m2
又底面正方形面积最小不得少于 ,
, ,所以,底面正方形的面积最小可取
,所以,底面正方形的面积最小可取
19.解:(Ⅰ) 令
令 得
得
当 为增函数;
为增函数;
当 为减函数,
为减函数,
可知 有极大值为
有极大值为
(Ⅱ)欲使 在
在 上恒成立,只需
上恒成立,只需 在
在 上恒成立,
上恒成立,
设
 由(Ⅰ)知,
由(Ⅰ)知, ,
,

(Ⅲ) ,由上可知
,由上可知 在
在 上单调递增,
上单调递增,
 ①,
①,
同理 ②
②
两式相加得

20.解:(1)证明:因为
所以 即
即
可化为:
当且仅当 即
即 时
时
故
(2)因为

=

=

又由 可知
可知 =
=

即 =
=

解之得 
故得 所以
所以

因此 的通项公式为..
的通项公式为..
(3)解:


所以
即S的最大值为
三、附加题
∵ÐDEF是公共角,
∴ΔDEF∽ΔCED. ∴ÐEDF=ÐC.
∵CD∥AP, ∴ÐC=Ð P.
∴ÐP=ÐEDF.
(2)∵ÐP=ÐEDF, ÐDEF=ÐPEA,
∴ΔDEF∽ΔPEA. ∴DE : PE=EF : EA.即EF?EP=DE?EA.
∵弦AD、BC相交于点E,∴DE?EA=CE?EB.∴CE?EB=EF?EP.
21B.法一:特殊点法
在直线 上任取两点(2、1)和(3、3),…………1分
上任取两点(2、1)和(3、3),…………1分
则 ?
?
 即得点
即得点 …………3 分
…………3 分

 即得点
即得点
将 和
和 分别代入
分别代入 上得
上得

则矩阵 …………6 分
…………6 分
则 …………10 分
…………10 分
法二:通法
设 为直线
为直线 上任意一点其在M的作用下变为
上任意一点其在M的作用下变为 …………1分
…………1分
则
 …………3分
…………3分
代入 得:
得:
 其与
其与 完全一样得
完全一样得
则矩阵 …………6分
…………6分
则 …………10分
…………10分
 化为
化为 , ………4分
, ………4分
 ,
………6分
,
………6分
设动点P ,M
,M ,则
,则  , ………8分
, ………8分
又  ,得
,得 ;
………10分
;
………10分
法二:以极点为坐标原点建立直角坐标系,
将直线方程 化为
化为 ,………………4分
,………………4分
设P ,M
,M ,
, ,………6分
,………6分
又MPO三点共线, ,
, …………8分
…………8分
转化为极坐标方程 . ………10分
. ………10分
21D.证明: ∵a、b、c均为实数.
∴ (
( +
+ )≥
)≥ ≥
≥ ,当a=b时等号成立;
,当a=b时等号成立;
 (
( +
+ )≥
)≥ ≥
≥ ,当b=c时等号成立;
,当b=c时等号成立;
 (
( +
+ )≥
)≥ ≥
≥ .
.
三个不等式相加即得 +
+ +
+ ≥
≥ +
+ +
+ ,
,
当且仅当a=b=c时等号成立.
22.解:(I)以O为原点,OB,OC,OA分别为x,y,z轴建立空间直角坐标系.
则有A(0,0,1),B(2,0,0),C(0,2,0),E(0,1,0).
 cos<
cos< >
> .
.
由于异面直线BE与AC所成的角是锐角,故其余弦值是 .
.
 (II)
(II) ,
, ,
,
设平面ABE的法向量为 ,
,
则由 ,
, ,得
,得
取n=(1,2,2),
平面BEC的一个法向量为n2=(0,0,1),
 .
.
由于二面角A-BE-C的平面角是n1与n2的夹角的补角,其余弦值是- .
.
23.解: 的所有可能取值有6,2,1,-2;
的所有可能取值有6,2,1,-2; ,
,
 ,
,
故 的分布列为:
的分布列为:

6
2
1
-2

0.63
0.25
0.1
0.02
(2)
(3)设技术革新后的三等品率为 ,则此时1件产品的平均利润为
,则此时1件产品的平均利润为

依题意, ,即
,即 ,解得
,解得 所以三等品率最多为
所以三等品率最多为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com