从某学校高三年级800名学生中随机抽取50名测量身高，据测量被抽取的学生的身高全部介于155cm和195cm之间，将测量结果按如下方式分成八组：第一组[155，160）．第二组[160，165）；…第八组[190，195]，图是按上述分组方法得到的条形图．


（1）根据已知条件填写下面表格：

组 别	1	2	3	4	5	6	7	8
样本数

（2）估计这所学校高三年级800名学生中身高在180cm以上（含180cm）的人数；
（3）在样本中，若第二组有1人为男生，其余为女生，第七组有1人为女生，其余为男生，在第二组和第七组中各选一名同学组成实验小组，问：实验小组中恰为一男一女的概率是多少？

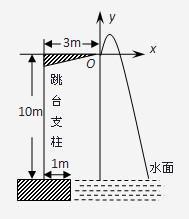某跳水运动员进行10米跳台跳水训练时，身体（看成一点）在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线（图中标出的数据为已知条件）．在跳某个规定动作时，正常情况下，该运动员在空中的最高处距水面10

2

3

米，入水处距池边的距离为4米，运动员在距水面高度为5米以前，必须完成规定的翻腾动作，并调整好入水姿势，否则就会出现失误．
（Ⅰ）求这条抛物线的解析式；
（Ⅱ）在某次试跳中，测得运动员在空中的运动路线是（Ⅰ）中的抛物线，且运动员在空中调整好入水姿势时，距池边的水平距离为3

3

5

米，问此次跳水会不会失误？并通过计算．

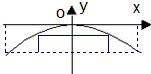一座抛物线拱桥在某时刻水面的宽度为52米，拱顶距离水面6.5米．
（1）建立如图所示的平面直角坐标系xoy，试求拱桥所在抛物线的方程；
（2）若一竹排上有一4米宽6米高的大木箱，问此木排能否安全通过此桥？