
题目列表(包括答案和解析)
| |||||||||||||||
| |||||||||||
已知幂函数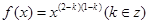 满足
满足 。
。
(1)求实数k的值,并写出相应的函数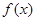 的解析式;
的解析式;
(2)对于(1)中的函数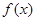 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数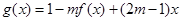 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
【解析】本试题主要考查了函数的解析式的求解和函数的最值的运用。第一问中利用,幂函数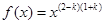 满足
满足 ,得到
,得到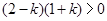
因为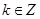 ,所以k=0,或k=1,故解析式为
,所以k=0,或k=1,故解析式为
(2)由(1)知,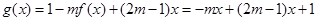 ,
, ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: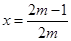 ,结合二次函数的对称轴,和开口求解最大值为5.,得到
,结合二次函数的对称轴,和开口求解最大值为5.,得到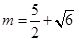
(1)对于幂函数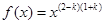 满足
满足 ,
,
因此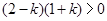 ,解得
,解得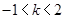 ,………………3分
,………………3分
因为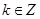 ,所以k=0,或k=1,当k=0时,
,所以k=0,或k=1,当k=0时, ,
,
当k=1时, ,综上所述,k的值为0或1,
,综上所述,k的值为0或1, 。………………6分
。………………6分
(2)函数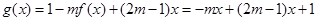 ,………………7分
,………………7分
由此要求 ,因此抛物线开口向下,对称轴方程为:
,因此抛物线开口向下,对称轴方程为: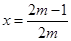 ,
,
当 时,
时,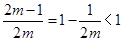 ,因为在区间
,因为在区间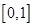 上的最大值为5,
上的最大值为5,
所以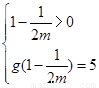 ,或
,或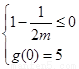 …………………………………………10分
…………………………………………10分
解得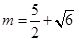 满足题意
满足题意
| |||||||||||||||
 水是生命之源、生产之要、生态之基.2010年春季,西南5省面临世纪大旱,5000多万同胞受灾.这场少见的世纪大旱使农作物受灾面积近500万公顷,其中40万公顷良田颗粒无收,2000万同胞面临无水可饮的绝境.某乡镇对此次旱灾进行了认真的分析、总结,决定建造一个容积为4800m3,深为3m的长方体形无盖贮水池,以解决当地居民饮水、灌溉问题.已知贮水池池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底一边长为xm,总造价为y(单位:元).
水是生命之源、生产之要、生态之基.2010年春季,西南5省面临世纪大旱,5000多万同胞受灾.这场少见的世纪大旱使农作物受灾面积近500万公顷,其中40万公顷良田颗粒无收,2000万同胞面临无水可饮的绝境.某乡镇对此次旱灾进行了认真的分析、总结,决定建造一个容积为4800m3,深为3m的长方体形无盖贮水池,以解决当地居民饮水、灌溉问题.已知贮水池池底每平方米的造价为150元,池壁每平方米的造价为120元.设池底一边长为xm,总造价为y(单位:元).湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com