
题目列表(包括答案和解析)
如图所示,一质量为m的物体系于长度分别为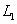 、
、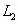 的两根细线上,
的两根细线上,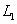 的一端悬挂在天花板上,与竖直方向夹角为
的一端悬挂在天花板上,与竖直方向夹角为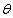 ,
,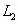 水平拉直,物体处于平衡状态.现将
水平拉直,物体处于平衡状态.现将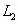 线剪断,求剪断瞬时物体的加速度.
线剪断,求剪断瞬时物体的加速度.
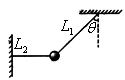
(1)下面是某同学对该题的一种解法:
分析与解:设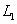 线上拉力为
线上拉力为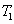 ,
,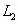 线上拉力为
线上拉力为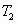 ,重力为mg,物体在三力作用下保持平衡,有
,重力为mg,物体在三力作用下保持平衡,有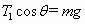 ,
,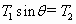 ,
,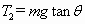
剪断线的瞬间,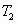 突然消失,物体即在
突然消失,物体即在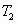 反方向获得加速度.因为
反方向获得加速度.因为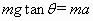 ,所以加速度
,所以加速度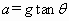 ,方向在
,方向在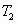 反方向.
反方向.
你认为这个结果正确吗?请对该解法作出评价并说明理由.
(2)若将图中的细线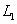 改为长度相同、质量不计的轻弹簧,如图所示,其他条件不变,求解的步骤和结果与(1)完全相同,即
改为长度相同、质量不计的轻弹簧,如图所示,其他条件不变,求解的步骤和结果与(1)完全相同,即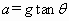 ,你认为这个结果正确吗?请说明理由.
,你认为这个结果正确吗?请说明理由.
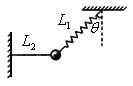
如图所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为q,l2水平拉直,物体处于平衡状态.现将l2线剪断,求剪断瞬时物体的加速度.
(1)下面是某同学对该题的一种解法:
c解:设l1线上拉力为T1,l2线上拉力为T2,重力为mg,物体在三力作用下保持平衡
T1cosq=mg,T1sinq =T2,T2=mgtanq
剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.因为mgtanq =ma,所以加速度a=gtanq,方向与T2反方向.
你认为这个结果正确吗?请对该解法作出评价并说明理由.
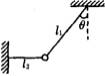
(2)若将图中的细线l1改为长度相同、质量不计的轻弹簧,如图所示,其他条件不变,求解的步骤和结果与(1)完全相同,即a=gtanq .你认为这个结果正确吗?请说明理由.

(1)下面是某同学对该题的一种解法:
c解:设l1线上拉力为T1,l2线上拉力为T2,重力为mg,物体在三力作用下保持平衡
T1cosq=mg,T1sinq =T2,T2=mgtanq
剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.因为mgtanq =ma,所以加速度a=gtanq,方向与T2反方向.
你认为这个结果正确吗?请对该解法作出评价并说明理由.
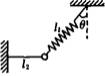
(2)若将图中的细线l1改为长度相同、质量不计的轻弹簧,如图所示,其他条件不变,求解的步骤和结果与(1)完全相同,即a=gtanq .你认为这个结果正确吗?请说明理由.

如图所示,一质量为m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为θ,l2水平拉直,物体处于平衡状态,现将l2线剪断,求剪断瞬间物体的加速度.

(1)下面是某同学对该题的一种解法.
解:设l1线上拉力为T1,l2上拉力为T2,重力为mg,物体在三力作用下保持平衡T1cosθ=mg T1sinθ=T2,T2=mgtanθ.
剪断线的瞬间,T2突然消失,物体即在T2反方向获得加速度.因为mgtanθ=ma,所以加速度a=gtanθ,方向在T2反方向.你认为这个结果正确吗?请对该解法作出评价并说明理由.
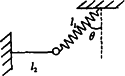
(2)若将图A中的细线l1改为长度相同、质量不计的轻质弹簧,如图B所示,其他条件不变,求解的步骤和结果与(1)完全相同,即a=gtanθ,你认为这个结果正确吗?请说明理由.
如图所示,一质量为
m的物体系于长度分别为l1、l2的两根细线上,l1的一端悬挂在天花板上,与竖直方向夹角为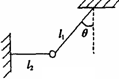
(1)下面是某同学对该题的一种解法:
解:设l1线上拉力为T1,线上拉力为T2,重力为mg,物体在三力作用下保持平衡
T1cos![]() =mg,T1sin
=mg,T1sin![]() =T2,T2=mgtg
=T2,T2=mgtg![]()
剪断线的瞬间,
T2突然消失,物体即在T2反方向获得加速度.因为mgtg你认为这个结果正确吗?请对该解法作出评价并说明理由.
(2)若将上图中的细线l1改为长度相同、质量不计的轻弹簧,如下图所示,其他条件不变,求解的步骤和结果与(l)完全相同,即a=gtg![]() ,你认为这个结果正确吗?请说明理由.
,你认为这个结果正确吗?请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com