
题目列表(包括答案和解析)
(18分)1957年第一颗人造卫星上天,开辟了人类宇航的新时代。四十多年来,人类不仅发射了人造地球卫星,还向宇宙空间发射了多个空间探测器。空间探测器要飞向火星等其它行星,甚至飞出太阳系,首先要克服地球对它的引力的作用。理论研究表明,由于物体在地球附近受到地球对它的万有引力的作用,具有引力势能。设质量为m的物体在距地球无限远处的引力势能为零,则引力势能表达式为EP=-![]() ,式中G是万有引力常量,M是地球的质量,r是该物体距地心的距离。
,式中G是万有引力常量,M是地球的质量,r是该物体距地心的距离。
(1)试证明空间探测器的最小发射速度与它绕地球匀速运行的最大环绕速度相等。
(2)现有一个质量为m的空间探测器绕地球做匀速圆周运动,运行周期为T,已知球半径为R,地面附近的重力加速度为g。求该探测器做匀速圆周运动时的机械能(用m、g、R、T表示);
(3)在(2)的情形下,要使这个空间探测器从运行轨道上出发,脱离地球的引力作用,至少要对它作多少功?
“重力探矿”是常用的探测石油矿藏的方法之一。其原理可简述如下:如图,P、Q为某地区水平地面上的两点,在P点正下方一球形区域内储藏有石油,假定区域周围岩石均匀分布,密度为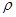 ;石油密度远小于
;石油密度远小于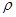 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。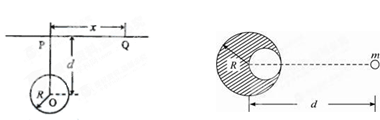
(1)“重力探矿”利用了“割补法”原理:如图所示,在一个半径为R、质量为M的均匀球体中,紧贴球的边缘挖去一个半径为R/2的球形空穴后,剩余的阴影部分对位于球心和空穴中心连线上、与球心相距d的质点m的引力是多大?
(2)设球形空腔体积为V,球心深度为d(远小于地球半径),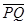 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为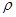 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力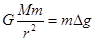 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值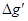 (
(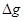 在OP方向上的分量)
在OP方向上的分量)
(3)若在水平地面上半径L的范围内发现:重力加速度反常值在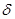 与
与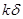 (k>1)(
(k>1)(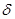 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
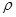 ;石油密度远小于
;石油密度远小于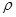 ,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
,可将上述球形区域视为空腔。如果没有这一空腔,则该地区重力加速度(正常值)沿竖直方向;当存在空腔时,该地区重力加速度的大小和方向会与正常情况有微小偏差。重力加速度在原坚直方向(即PO方向)上的投影相对于正常值的偏离叫做“重力加速度反常”。为了探寻石油区域的位置和石油储量,常利用P点附近重力加速度反常现象。已知引力常数为G。
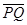 =x,利用“割补法”原理:如果将近地表的球形空腔填满密度为
=x,利用“割补法”原理:如果将近地表的球形空腔填满密度为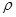 的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力
的岩石,则该地区重力加速度便回到正常值.因此,重力加速度反常值可通过填充后的球形区域对Q处物体m产生的附加引力 来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值
来计算,式中M是填充岩石后球形区域的质量,求空腔所引起的Q点处的重力加速度反常值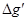 (
(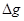 在OP方向上的分量)
在OP方向上的分量)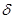 与
与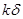 (k>1)(
(k>1)(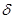 为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。
为常数)之间变化,且重力加速度反常的最大值出现在半为L的范围的中心,如果这种反常是由于地下存在某一球形空腔造成的,试求此球形空腔球心的深度和空腔的体积。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com