
题目列表(包括答案和解析)
如图15所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子又不可伸长,求平衡时弦AB所对的圆心角θ的一半的正弦值,即![]()
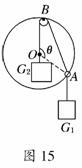
(12分)如图15所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子又不可伸长,求平衡时弦AB所对的圆心角θ.
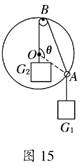
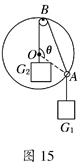
(12分)如图15所示,光滑小圆环A吊着一个重为G1的砝码套在另一个竖直放置的大圆环上,今有一细绳拴在小圆环A上,另一端跨过固定在大圆环最高点B处的一个小滑轮后吊着一个重为G2的砝码,如果不计小环、滑轮、绳子的重量大小.绳子又不可伸长,求平衡时弦AB所对的圆心角θ.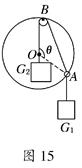
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com