指出下列事件是必然事件、不可能事件还是随机事们．

(1)如果a＞b，那么a—b＞0；

(2)将一枚硬币连掷三次，结果出现三次正面；

(3)三个小球全部放入两个盒中，其中一个盒子有一个以上的小球；

(4)直线Ax＋By＋C=0左侧区域内的点的坐标可使不等式Ax＋By＋C＞0成立；

(5)若xÎ R，则．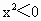

指出下列事件是必然事件、不可能事件还是随机事们．

(1)如果a＞b，那么a——b＞0；

(2)将一枚硬币连掷三次，结果出现三次正面；

(3)三个小球全部放入两个盒中，其中一个盒子有一个以上的小球；

(4)直线Ax＋By＋C=0左侧区域内的点的坐标可使不等式Ax＋By＋C＞0成立；

(5)若xÎ R，则．

记事件A发生的概率为P(A)，定义f(A)=[P(A)+]为事件A 发生的“测度”.现随机抛掷一个骰子，则下列事件中测度最大的一个是(      ).

A.向上的点数为1                B.向上的点数不大于2 

C.向上的点数为奇数              D.向上的点数不小于3

记事件A发生的概率为，定义(A)=[+]为事件A 发生的“测度”.现随机抛掷一个骰子，则下列事件中测度最大的一个是  （    ）

A. 向上的点数为1                    B. 向上的点数不大于2

C. 向上的点数为奇数                 D. 向上的点数不小于3

IF a<10 THEN y=2*a else y=a*a PRINT y End

用2×2列联表对两个事件的独立性检验中，统计量x²有两个临界值：3.841和6.635．当x²＞3.841时，有95%的把握说明两个变量有关；当x²＞6.635时，有99%的把握说明两个变量有关．为了探究家庭旅行兴趣与是否有车有关，随机抽查了100个家庭，按是否有车和旅行兴趣是否高进行调查，结果如下表：

	有车	无车	总计
兴趣高	45	20	65
兴趣不高	15	20	35
总计	60	40	100

根据调查结果计算x²的值，并根据计算结果说明所得到的结论．
（公式：x2=

n(n11n22-n12n21)2

n1+n2+n+1n+2

，计算结果精确到0.001）