
题目列表(包括答案和解析)
如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题:

(1)最初到达离家最远的地方是什么时间?离家多远?
(2)何时开始第一次休息?休息多长时间?
(3)第一次休息时,离家多远?
(4)11:00到12:00他骑了多少千米?
(5)他在9:00~10:00和10:00~10:30的平均速度分别是多少?
(6)他在哪段时间里停止前进并休息用午餐?

(1)应怎样画出它在地面上的投影?它的投影是一个什么样的三角形?
(2)若光源S慢慢远离正三角形ABC时,它在地面上的投影有何变化?
(3)当光源S趋近于无限远时,正三角形ABC和它在地面上的投影有何关系?
(4)你从中能领悟出中心投影与平行投影之间有何关系?
如图所示,水平放置的正三角形ABC,在它的正上方有光源S.请探究如下问题.
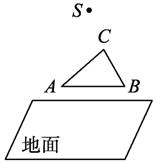
(1)应怎样画出它在地面上的投影?它的投影是一个什么样的三角形?
(2)若光源S慢慢远离正三角形ABC时,它在地面上的投影有何变化?
(3)当光源S趋近于无限远时,正三角形ABC和它在地面上的投影有何关系?
(4)你从中能领悟出中心投影与平行投影之间有何关系?

(1)应怎样画出它在地面上的投影?它的投影是一个什么样的三角形?
(2)若光源S慢慢远离正三角形ABC时,它在地面上的投影有何变化?
(3)当光源S趋近于无限远时,正三角形ABC和它在地面上的投影有何关系?
(4)你从中能领悟出中心投影与平行投影之间有何关系?
图的曲线表示一个骑自行车离家的距离与时间的关系.骑车者
9时离开家,15时回家,根据这个曲线图,请你回答下列问题: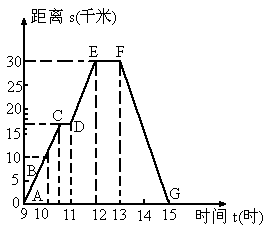
(1)最初到达离家最远的地方是什么时间?离家多远?
(2)
何时开始第一次休息?休息多长时间?(3)
第一次休息时,离家多远?(4)1
1∶00到12∶00他骑了多少千米?(5)
他在9∶00~10∶00和10∶00~10∶30的平均速度分别是多少?(6)
他在哪段时间里停止前进并休息用午餐?湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com