
题目列表(包括答案和解析)
【解析】若![]() ,必有
,必有![]() .构造函数:
.构造函数:![]() ,则
,则![]() 恒成立,故有函数
恒成立,故有函数![]() 在x>0上单调递增,即a>b成立.其余选项用同样方法排除.
在x>0上单调递增,即a>b成立.其余选项用同样方法排除.
【答案】A
函数f(x)=cos2x+sinxcosx的最大值是( )
A.2 B. C.
C. D.
D.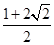
[答案] C
[解析]
(本小题满分12分)设函数 (a为实数).
(a为实数).
(1)若a<0,用函数单调性定义证明: 在
在 上是增函数;
上是增函数;
(2)若a=0, 的图象与
的图象与 的图象关于直线y=x对称,求函数
的图象关于直线y=x对称,求函数 的解析式.
的解析式.
5.A解析:因为函数有0,1,2三个零点,可设函数为f(x)=ax(x-1)(x-2)=ax3-3ax2+2ax
因此b=-3a,又因为当x>2时f(x)>0所以a>0,因此b<0
在15个村庄中有7个村庄交通不方便,现从中任意选10个,用X表示这10个村庄中交通方便的村庄数,若![]() ,则a= .
,则a= .
已知点A(7,1),B(1,4),若直线y=ax与线段AB交于点C,且 =2
=2 ,则实数a=________.
,则实数a=________.
[答案] 1
[解析] 设C(x0,ax0),则 =(x0-7,ax0-1),
=(x0-7,ax0-1), =(1-x0,4-ax0),
=(1-x0,4-ax0),
∵ =2
=2 ,∴
,∴ ,解之得
,解之得 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com