题目列表(包括答案和解析)
直线l：y=k（x-1）过已知椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
| MA |
| AF |
| MB |
| BF |
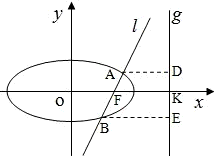直线l：y=k（x-1）过已知椭圆
经过点（0，
），离心率为
，经过椭圆C的右焦点F的直线l交椭圆于A、B两点，点A、F、B在直线x=4上的射影依次为点D、K、E．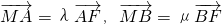
，当直线l的倾斜角变化时，探求λ+μ的值是否为定值？若是，求出λ+μ的值，否则，说明理由；| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 1 |
| 2 |
| MA |
| AF |
| MB |
| BF |
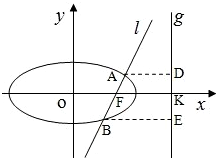
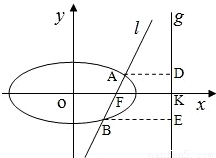直线l：y=k（x-1）过已知椭圆
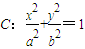经过点（0，
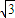），离心率为
，经过椭圆C的右焦点F的直线l交椭圆于A、B两点，点A、F、B在直线x=4上的射影依次为点D、K、E．
，当直线l的倾斜角变化时，探求λ+μ的值是否为定值？若是，求出λ+μ的值，否则，说明理由；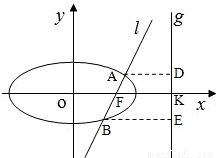
直线l：y=k（x-1）过已知椭圆
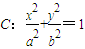经过点（0，
），离心率为
，经过椭圆C的右焦点F的直线l交椭圆于A、B两点，点A、F、B在直线x=4上的射影依次为点D、K、E．
，当直线l的倾斜角变化时，探求λ+μ的值是否为定值？若是，求出λ+μ的值，否则，说明理由；一、选择题：
1―5：BABDD 6―10:BABDC 11―12:AC
二、填空题：
13、1 14、
15、
16、①③④
三、解答题：
17、解：（Ⅰ）
……………………（2分）
即
即
………………………………………………………………（4分）
由于
，故
…………………………………………………（6分）
(Ⅱ)由
知
，
…………………………………………………………（8分）
…………（10分）
当且仅当
，即
时，
取得最大值
.
所以
的最大值为
，此时
为等腰三角形.
18、解析：（1）抽取的4根钢管中恰有2根长度相同的概率为：
……………………………………………………………………（3分）
（2）新焊接成钢管的长度的可能值有7种，最短的可能值为5m，最长的可能值为11m.
当
=5m与=11m时的概率为
；
当=6m与=10m时的概率为
；tesoon
当=7m与=9m时的概率为
；
当=8m时的概率为
.…………………………………………（9分）
的分布列为：
5
6
7
8
9
10
11
…………………………（12分）
19、（1）圆
，当
时，点
在圆上，故当且仅当直线
过圆心C时满足
.
圆心坐标为（1，1），
…………………………………………………………（3分）
（2）由
，消去
可得
.
得
………………①
设
，则
……………………………………（5分）
，即
=0.
又
，
，即
.
.
故
…………………………………………………………………………（9分）
又
（当且仅当时取=）
即
………………②
由①②知，
直线的倾斜角取值范围为：
…………………………………………………（12分）
20、解：（1）设
，
（
）
在[-1,1]上是增函数………………………………………（3分）
（2）
，解得：
…………………………（7分）
（3）对所有
恒成立，等价于
的最大值不大于
.
又
在[-1,1]上是增函数，在[-1,1]上的最大值为
即
,得
，
设
，是关于
的一次函数，要使
恒成立，
只需
即可，解得：
或
或
.
21、解析：（1）设
在
处有极值，
即
在点（0，-3）处的切线平行于
即
故
…………………………………………………………………（4分）
（2）设
又
时，
(递减)
时，
（递增）
曲线
上任意两点的连线的斜率恒大于
.
解不等式
得
.
或
…………………………………………………………（8分）
（3）设
，则
，
时
为[0,1]上的增函数
的值域是[-4. 
].…………………………（12分）
22、解析：（1）圆
与
彼此外切，令
为圆的半径，
即
，
两边平方并化简得
，
由题意得，圆的半径
，
即
……………………………………………………………………（5分）
数列
是以
为首项，以2为公差的等差数列，
所以
即
.………………………………………………（8分）
（2）
，……………………………………………………（10分）
因为
…………………………………………………（12分）
所以
………………………………………………………………………………（14分）
天星教育网（www.tesoon.com） 版权所有
天星教育网（www.tesoon.com） 版权所有
天星教育网（www.tesoon.com） 版权所有
|
