
题目列表(包括答案和解析)
(10分)如图所示,AB是一段位于竖直平面内的弧形轨道,高度为h,末端B处的切线沿水平方向。一个质量为m的小物体P(可视为质点)从轨道顶端处A点由静止释放,滑到B点时以水平速度v飞出,落在水平地面的C点,其轨迹如图中虚线BC所示。已知P落地时相对于B点的水平位移OC= l,重力加速度为g,不计空气阻力的作用。

(1)请计算P在弧形轨道上滑行的过程中克服摩擦力所做的功;
(2)现于轨道下方紧贴B点安装一水平传送带,传送带右端E轮正上方与B点相距。先将驱动轮锁定,传送带处于静止状态。使P仍从A点处由静止释放,它离开B点后先在传送带上滑行,然后从传送带右端水平飞出,恰好仍落在地面上C点,其轨迹如图中虚线EC所示。若将驱动轮的锁定解除,并使驱动轮以角速度ω顺时针匀速转动,再使P仍从A点处由静止释放,最后P的落地点是D点(图中未画出)。已知驱动轮的半径为r,传送带与驱动轮之间不打滑,且传送带的厚度忽略不计。求:
①小物块P与传送带之间的动摩擦因数;
②若驱动轮以不同的角速度匀速转动,可得到与角速度ω对应的OD值,讨论OD的可能值与ω的对应关系。
(10分)如图所示,AB是一段位于竖直平面内的弧形轨道,高度为h,末端B处的切线沿水平方向。一个质量为m的小物体P(可视为质点)从轨道顶端处A点由静止释放,滑到B点时以水平速度v飞出,落在水平地面的C点,其轨迹如图中虚线BC所示。已知P落地时相对于B点的水平位移OC=l,重力加速度为g,不计空气阻力的作用。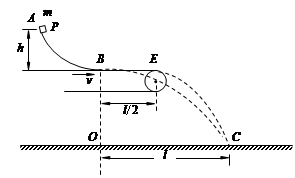
(1)请计算P在弧形轨道上滑行的过程中克服摩擦力所做的功;
(2)现于轨道下方紧贴B点安装一水平传送带,传送带右端E轮正上方与B点相距。先将驱动轮锁定,传送带处于静止状态。使P仍从A点处由静止释放,它离开B点后先在传送带上滑行,然后从传送带右端水平飞出,恰好仍落在地面上C点,其轨迹如图中虚线EC所示。若将驱动轮的锁定解除,并使驱动轮以角速度ω顺时针匀速转动,再使P仍从A点处由静止释放,最后P的落地点是D点(图中未画出)。已知驱动轮的半径为r,传送带与驱动轮之间不打滑,且传送带的厚度忽略不计。求:
①小物块P与传送带之间的动摩擦因数;
②若驱动轮以不同的角速度匀速转动,可得到与角速度ω对应的OD值,讨论OD的可能值与ω的对应关系。
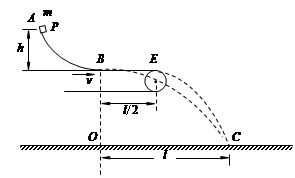
(23分)有一带活塞的气缸,如图1所示。缸内盛有一定质量的气体。缸内还有一可随轴转动的叶片,转轴伸到气缸外,外界可使轴和叶片一起转动,叶片和轴以及气缸壁和活塞都是绝热的,它们的热容量都不计。轴穿过气缸处不漏气。

图1
如果叶片和轴不转动,而令活塞缓慢移动,则在这种过程中,由实验测得,气体的压强![]() 和体积
和体积![]() 遵从以下的过程方程式
遵从以下的过程方程式
![]()
其中![]() ,
,![]() 均为常量,
均为常量, ![]() >1(其值已知)。可以由上式导出,在此过程中外界对气体做的功为
>1(其值已知)。可以由上式导出,在此过程中外界对气体做的功为

式中![]() 和
和![]() ,分别表示末态和初态的体积。
,分别表示末态和初态的体积。
如果保持活塞固定不动,而使叶片以角速度![]() 做匀角速转动,已知在这种过程中,气体的压强的改变量
做匀角速转动,已知在这种过程中,气体的压强的改变量![]() 和经过的时间
和经过的时间![]() 遵从以
遵从以
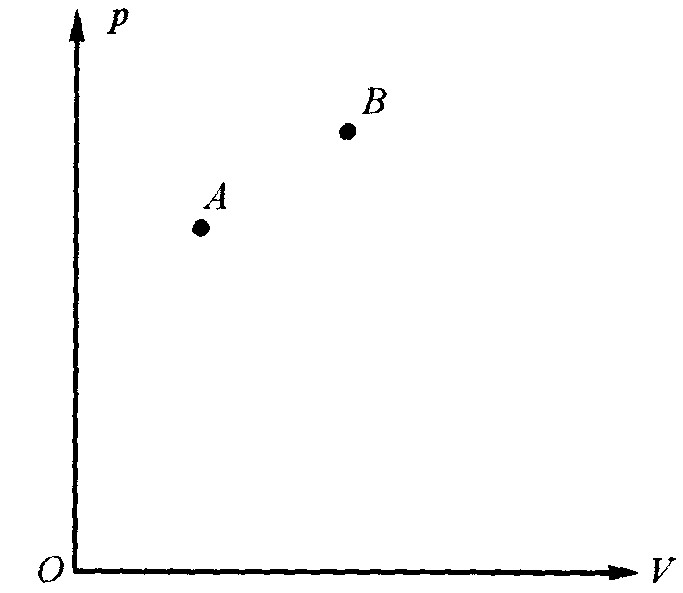
图2
下的关系式
![]()
式中![]() 为气体的体积,
为气体的体积,![]() 表示气体对叶片阻力的力矩的大小。
表示气体对叶片阻力的力矩的大小。
上面并没有说气体是理想气体,现要求你不用理想气体的状态方程和理想气体的内能只与温度有关的知识,求出图2中气体原来所处的状态![]() 与另一已知状态
与另一已知状态![]() 之间的内能之差(结果要用状态
之间的内能之差(结果要用状态![]() 、
、![]() 的压强
的压强![]() 、
、![]() 和体积
和体积![]() 、
、![]() 及常量
及常量![]() 表示)
表示)
将一个质量为1kg的小球竖直向上抛出,最终落回抛出点,运动过程中所受阻力大小恒定,方向与运动方向相反。该过程的v-t图象如图所示,g取10m/s2。下列说法中正确的是
A.小球上升与下落所用时间之比为2∶3
B.小球下落过程,处于失重状态
C.小球上升过程中克服阻力做功48 J
D.小球上升过程中机械能的损失大于下落过程中的机械能损失

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com