
题目列表(包括答案和解析)
(本题12分)某地区上年度电价为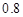 元/kW•h,年用电量为
元/kW•h,年用电量为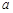 kW•h.本年度计划将电价降低到0.55元/ kW•h到0.75元/ kW•h之间,而用户期望电价为0.40元/ kW•h.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为
kW•h.本年度计划将电价降低到0.55元/ kW•h到0.75元/ kW•h之间,而用户期望电价为0.40元/ kW•h.经测算,下调电价后新增用电量与实际电价与用户的期望电价的差成反比(比例系数为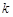 ),该地区电力的成本价为0.30元/ kW•h.
),该地区电力的成本价为0.30元/ kW•h.
(1)写出本年度电价下调后,电力部门的收益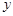 与实际电价
与实际电价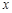 之间的函数关系式;
之间的函数关系式;
(2)设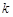 =
=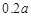 ,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价
,当电价最低定为多少时仍可保证电力部门的收益比上一年至少增长20%?(注:收益=实际电量×(实际电价 本价))
本价))
某休闲场馆举行圣诞酬宾活动,每位会员交会员费50元,可享受20元的消费,并参加一次抽奖活动,从一个装有标号分别为1,2,3,4,5,6的6只均匀小球的抽奖箱中,有放回的抽两次球,抽得的两球标号之和为12,则获一等奖价值a元的礼品,标号之和为11或10,获二等奖价值100元的礼品,标号之和小于10不得奖.
(1)求各会员获奖的概率;
(2)设场馆收益为ξ元,求ξ的分布列;假如场馆打算不赔钱,a最多可设为多少元?
(本题满分16分)
 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形 和
和 构成的面积为200
构成的面积为200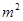 的十字型地域,计划在正方形
的十字型地域,计划在正方形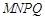 上建一座“观景花坛”,造价为4200元
上建一座“观景花坛”,造价为4200元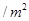 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元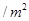 ,再在四个空角(如
,再在四个空角(如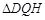 等)上铺草坪,造价为80元
等)上铺草坪,造价为80元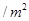 .设
.设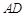 长为
长为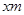 ,
,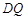 长为
长为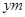 .
.
(1)试找出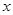 与
与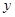 满足的等量关系式;
满足的等量关系式;
(2)设总造价为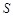 元,试建立
元,试建立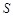 与
与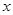 的函数关系;
的函数关系;
(3)若总造价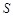 不超过138000元,求
不超过138000元,求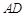 长
长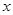 的取值范围.
的取值范围.
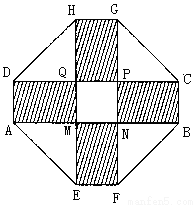
某小区要建一座八边形的休闲小区,它的主体造型的平面图是由二个相同的矩形
和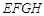 构成的面积为
构成的面积为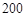
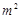 的十字型地域,计划在正方形
的十字型地域,计划在正方形 上建一座“观景花坛”,
上建一座“观景花坛”,
造价为 元/
元/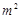 ,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为
,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为

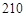 元/
元/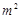 ,再在四个空角(如
,再在四个空角(如 等)上铺草坪,造价为
等)上铺草坪,造价为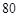 元/
元/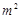 .
.
(1)设总造价为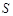 元,
元,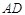 长为
长为
 ,试建立
,试建立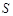 与
与 的函数关系;
的函数关系;
(2)当 为何值时,
为何值时,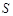 最小?并求这个最小值。
最小?并求这个最小值。
(本题满分16分)
2010年上海世博会某国要建一座八边形(不一定为正八边形)的展馆区(如图),它的主体造型的平面图是由二个相同的矩形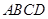 和
和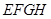 构成的面积为
构成的面积为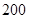 m2的十字型地域,计划在正方形
m2的十字型地域,计划在正方形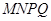 上建一座“观景花坛”,造价为
上建一座“观景花坛”,造价为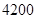 元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为
元/m2,在四个矩形上(图中阴影部分)铺花岗岩地坪,造价为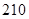 元/m2,再在四个空角(如
元/m2,再在四个空角(如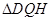 等)上铺草坪,造价为
等)上铺草坪,造价为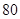 元/m2. 设总造价为
元/m2. 设总造价为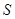 元,
元,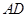 长为
长为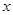 m.
m.
 (1)用
(1)用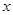 表示矩形
表示矩形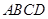 的边
的边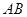 的长
的长
(1)试建立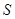 与
与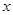 的函数关系
的函数关系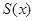
(2)当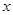 为何值时,
为何值时,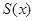 最小?并求这个最小值
最小?并求这个最小值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com