
题目列表(包括答案和解析)
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x |
| 1 |
| 3 |
 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队施工速度快?
,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队施工速度快? ,那么甲队半个月完成总工程的________,设乙队单独施工1个月能完成总工程的
,那么甲队半个月完成总工程的________,设乙队单独施工1个月能完成总工程的 ,那么乙队半个月完成总工程的________(用含x的代数式表示),两队半个月完成总工程的________(用含x的代数式表示).
,那么乙队半个月完成总工程的________(用含x的代数式表示),两队半个月完成总工程的________(用含x的代数式表示). ,可知________队施工速度快.
,可知________队施工速度快. ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队施工速度快?
,这时增加了乙队,两队又共同工作了半个月,总工程全部完成.哪个队施工速度快? ,那么甲队半个月完成总工程的______,设乙队单独施工1个月能完成总工程的
,那么甲队半个月完成总工程的______,设乙队单独施工1个月能完成总工程的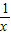 ,那么乙队半个月完成总工程的______(用含x的代数式表示),两队半个月完成总工程的______(用含x的代数式表示).
,那么乙队半个月完成总工程的______(用含x的代数式表示),两队半个月完成总工程的______(用含x的代数式表示). ,可知______队施工速度快.
,可知______队施工速度快.| 工作效率 | 工作时间 | 工作量 | |||||
| 甲 |
|
1 |
| ||||
| 乙 | x | 1 | |||||
| 甲、乙合作 |
|
| 1 |
| x |
| 1 |
| x |
| 1 |
| x+10 |
| 1 |
| x+10 |
| 8 |
| x |
| x |
| x+10 |
| 8 |
| x |
| x |
| x+10 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com