
题目列表(包括答案和解析)
下列方程解法对吗?
解方程![]() .
.
解:方程两边同时乘以(x+1)(x-1)得
2(x-1)+3(x+1)=6.
解这个整式方程,得x=1.
所以原方程的解为x=1.
题目:解方程![]() .
.
解:方程两边同乘以(x+2)(x-2)得 (A)
(x+2)(x-2)![]() =-
=-![]() ·(x+2)(x-2).
·(x+2)(x-2).
化简,得(x-2)+4x=2(x+2). (B)
去括号,移项,得x-2+4x-2x-4=0. (C)
解这个方程得x=2. (D)
∴x=2是原方程的解. (E)
问题:(1)上述过程是否正确?答________.
(2)若有错误,错在________.
(3)该步错误的原因是________.
(4)该步改正为________.
阅读下列材料:
解方程![]() .
.
解:方程两边同乘x-2,约去分母,得
1=x-1-3(x-2)
解这个整式方程,得x=2.
所以,原方程的解为x=2.
根据以上材料,回答下列问题:
(1)以上解答是否有错误,若有错误,指出错误,并改正;
(2)请你根据这个方程的特点,用另外一种方法解答.
观察可得最简公分母是(x+1)(x-1),方程两边乘最简公分母,可以把分式方程转化为整式方程求解.
【解答】
(2)方程的两边同乘(x+1)(x-1),得
2(x-1)+4=x2-1,
即x2-2x-3=0,
(x-3)(x+1)=0,
解得x1=3,x2=-1,
检验:把x=3代入(x+1)(x-1)=8≠0,即x=3是原分式方程的解,
把x=-1代入(x+1)(x-1)=0,即x=-1不是原分式方程的解,
则原方程的解为:x=3.
【点评】此题考查了![]() 实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
实数的混合运算与分式方程的解法.此题难度不大,但注意掌握绝对值的性质、负指数幂的性质、零指数幂的性质以及特殊角的三角函数值,注意解分式方程一定要验根.
20.(本题满分5分)如图,已知△ABC,且∠ACB=90°。
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明);
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系(不必证明).
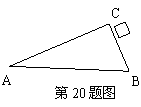 |
大家知道,解分式方程的基本方法是,把方程的两边同乘以各分母的最简公分母,化为整式方程来解,而对于一些特殊的分式方程来说,采用上述方法往往越解越繁.下面我们介绍一种简捷、明快的方法--拆项法.
例:解方程![]()
解:先降低方程中各分式分子的次数,将原方程变形为![]()
即(4+![]() )-(7+
)-(7+![]() )=(1-
)=(1-![]() )-(4-
)-(4-![]() )
)
整理得![]()
两边各自通分得
![]()
∴(x-2)(x-1)=(x-7)(x-6)
即x2-3x+2=x2-13x+42
也即10x=40 ∴x=4
经检验知,x=4是原方程的根.
请你运用上述方法,解分式方程
![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com