
题目列表(包括答案和解析)
(16分)一个公差不为零的等差数列{an}共有100项,首项为5,其第1、4、16项分别为正项等比数列{bn}的第1、3、5项. 记{an}各项和的值为S.
⑴求S (用数字作答);
⑵若{bn}的末项不大于![]() ,求{bn}项数的最大值N;
,求{bn}项数的最大值N;
⑶记数列![]() ,
,![]() .求数列
.求数列![]() 的前
的前![]() 项的和
项的和![]() .
.
| 分组(分数段) | 频数(人数) | 频率 |
| (60,70) | 8 8 |
0.16 |
| (70,80) | 22 | 0.44 0.44 |
| (80,90) | 14 | 0.28 |
| (90,100) | 6 6 |
0.12 0.12 |
| 合计 | 50 | 1 1 |
(本题16分)
如图所示,某人在斜坡P处仰视正对 面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为
面山顶上一座铁塔,塔高AB=80米,塔所在山高OA=220米,OC=200米,观测者所在斜坡CD近似看成直线,斜坡与水平面夹角为 ,
,
(1)以射线OC为 轴的正向,OB为
轴的正向,OB为 轴正向,建立直角坐标系,求
轴正向,建立直角坐标系,求 出斜坡CD所在直线方程;
出斜坡CD所在直线方程;
(2)当观察者P视角∠APB最大时,求点P的坐标(人的身高忽略不计).
(本小题满分16分)
已知等差数列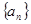 中,
中,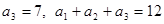 ,令
,令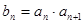 ,数列
,数列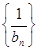 的前
的前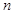 项和为
项和为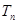 .
.
(1)求数列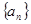 的通项公式;
的通项公式;
(2)求证: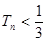 ;
;
(3)是否存在正整数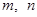 ,且
,且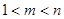 ,使得
,使得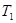 ,
,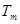 ,
,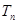 成等比数列?若存在,求出
成等比数列?若存在,求出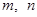 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本题满分16分;第(1)小题5分,第(2)小题5分,第(3)小题6分)
设![]() 、
、![]() 为坐标平面
为坐标平面![]() 上的点,直线
上的点,直线![]() (
(![]() 为坐标原点)与抛物线
为坐标原点)与抛物线![]() 交于点
交于点![]() (异于
(异于![]() ).
).
若对任意![]()
![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,试问当
上,试问当![]() 为何值时,点
为何值时,点![]() 在某一圆上,并求出该圆方程
在某一圆上,并求出该圆方程![]() ;
;
若点![]() 在椭圆
在椭圆![]() 上,试问:点
上,试问:点![]() 能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
能否在某一双曲线上,若能,求出该双曲线方程,若不能,说明理由;
对(1)中点![]() 所在圆方程
所在圆方程![]() ,设
,设![]() 、
、![]() 是圆
是圆![]() 上两点,且满足
上两点,且满足![]() ,试问:是否存在一个定圆
,试问:是否存在一个定圆![]() ,使直线
,使直线![]() 恒与圆
恒与圆![]() 相切.
相切.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com