
题目列表(包括答案和解析)

| A.环滚上的高度小于h |
| B.环滚上的高度等于h |
| C.由于环在作切割磁感线运动,故环中有感应电流产生 |
| D.环损失的机械能等于环产生的焦耳热 |
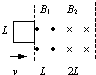 两个有界匀强磁场的方向均垂直于纸面,宽度分别为L和2L,磁感应强度大小B1=B2,但方向相反;有一边长为L的正方形导线框,在外力F作用下匀速通过整个磁场,如图所示.设感应电流逆时针方向为正向,F为拉动线圈的外力,从线圈刚进入B1的磁场开始计位移,线圈中感应电流i与外力F随位移x的变化情况如选项中所示,其中正确的是( )
两个有界匀强磁场的方向均垂直于纸面,宽度分别为L和2L,磁感应强度大小B1=B2,但方向相反;有一边长为L的正方形导线框,在外力F作用下匀速通过整个磁场,如图所示.设感应电流逆时针方向为正向,F为拉动线圈的外力,从线圈刚进入B1的磁场开始计位移,线圈中感应电流i与外力F随位移x的变化情况如选项中所示,其中正确的是( ) 处在非匀强磁场中的闭合金属环从曲面上h高处滚下,又沿曲面的另一侧上升到最大高度,设环的初速度为零,摩擦不计,曲面处在如图所示的磁场中,则此过程中( )
处在非匀强磁场中的闭合金属环从曲面上h高处滚下,又沿曲面的另一侧上升到最大高度,设环的初速度为零,摩擦不计,曲面处在如图所示的磁场中,则此过程中( )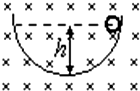 处在非匀强磁场中的闭合金属环从曲面上h高处滚下,又沿曲面的另一侧上升到最大高度,设环的初速度为零,摩擦不计,曲面处在图所示的非匀强磁场中,则此过程中( )
处在非匀强磁场中的闭合金属环从曲面上h高处滚下,又沿曲面的另一侧上升到最大高度,设环的初速度为零,摩擦不计,曲面处在图所示的非匀强磁场中,则此过程中( )| A、环滚上的高度小于h | B、环滚上的高度等于h | C、环中无感应电流产生 | D、环损失的机械能大于环产生的焦耳热 |
处在非匀强磁场中的闭合金属环从曲面上h高处滚下,又沿曲面的另一侧上升到最大高度,设环的初速度为零,摩擦不计,曲面处在图8所示的磁场中,则此过程中:
A.环滚上的高度小于h;
B.环滚上的高度等于h;
C.环中无感应电流产生;
D.环损失的机械能等于环产生的焦耳热。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com