练习册

  • 练习册
  • 试题
    C(整体把握文章.依相关中心句的表述可得) 【查看更多】

     

    题目列表(包括答案和解析)

    (1)列举法：把集合中的元素　　　　　出来，写在　　　　　内表示集合的方法.列举法表示集合的特点是清晰、直观.集合中元素的个数较少时常适用于列举法.?

    (2)描述法：把集合中的元素　　　　　的描述出来，写在　　　　　内表示集合的方法.一般形式是{x|p}，其中竖线前面的x叫做此集合的代表元素，竖线后面的p指出元素x所具有的公共属性.描述法便于从整体上把握一个集合，常适用于集合中元素的公共属性较为明显时.

    (3)韦恩图：为了形象地表示集合，有时常用一些封闭的　　　　　表示一个集合，这样的图形称为韦恩图，在解题时，利用韦恩图“数”和“形”结合，使得解答十分直观.?

    如集合A={a，b，c}可形象地表示为图(1)或图(2).?

                            (1)　　　　            　　(2)

    查看答案和解析>>

    现对某市工薪阶层关于“楼市限购令”的态度进行调查，随机抽调了50人，他们月收入的频数分布及对楼市“楼市限购令”赞成人数如下表．
    月收入（单位百元） [15，25） [25，35） [35，45） [45，55） [55，65） [65，75）
    频数 5 10 15 10 5 5
    赞成人数 4 8 12 5 2 1
    （Ⅰ）由以上统计数据填下面2乘2列联表并问是否有99%的把握认为“月收入以5500为分界点对“楼市限购令”的态度有差异；
    月收入不低于55百元的人数 月收入低于55百元的人数 合计
    赞成 a= c=
    不赞成 b= d=
    合计
    （Ⅱ）若对在[15，25），[25，35）的被调查中各随机选取两人进行追踪调查，记选中的4人中不赞成“楼市限购令”人数为ξ，求随机变量ξ的分布列及数学期望．
    参考公式：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    ，其中n=a+b+c+d．
    参考值表：
    P（K^2≥k） 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828

    查看答案和解析>>

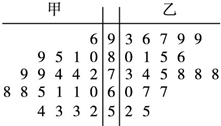    精英家教网某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下．记成绩不低于90分者为“成绩优秀”．
    （Ⅰ）在乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
    （Ⅱ）由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关．
    附：K2=
    n(ad-bc)2
    (a+b)(c+d)(a+c)(b+d)
    （此公式也可写成x2=
    n(n11 n22-n12n21)2
    n1+ n2+n+1n+2
    ）
    P（k2≥K） 0.25 0.15 0.10 0.05 0.025
    k 1.323 2.072 2.706 3.841 5.024

    查看答案和解析>>

    （2013•临沂一模）某校为了研究学生的性别和对待某一活动的态度（支持和不支持两种态度）的关系，运用2×2列联表进行独立性检验，经计算K2=7.069，则所得到的统计学结论是：有（　　）的把握认为“学生性别与支持该活动有关系”．
    P（k2≥k0） 0.100 0.050 0.025 0.010 0.001
    k0 2.706 3.841 5.024 6.635 10.828

    查看答案和解析>>

    随着生活水平的提高，儿童的身高越来越成为人们关注的话题，某心理研究机构从边区某小学四年级学生中随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．
    （1）现先用分层抽样的方法从各组中共选取20人作为样本，然后再从第四组或第五组选出的人中选出两人进行进一步分析，则这两人来自不同组的概率是多少？
    （2）若将身高超过130cm称为正常，低于130cm称为偏低，抽出的20名学生按性别与身高统计具体分布情况如下：
    男 女
    正常 2 5
    偏低 10 3
    用假设检验的方法分析：有多大的把握认为该年级学生的身高是否正常与性别有关？
    P（K2≥k） 0.15 0.10 0.05 0.025 0.010 0.005 0.001
    k 2.07 2.71 3.84 5.02 6.64 7.88 10.83
    参考公式及数据K2=
    n(ad-bc)2
    (a+c)(b+d)(a+b)(c+d)
    ．

    查看答案和解析>>


    同步练习册答案