
题目列表(包括答案和解析)
| a |
| x |
| a |
| a |
| 2b |
| x |
| c |
| x2 |
| a |
| x |
| c |
| x2 |
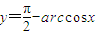 是奇函数;
是奇函数;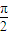 是sinA<cosB的充要条件;
是sinA<cosB的充要条件;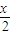 -
- )的图象,只需将y=sin
)的图象,只需将y=sin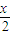 的图象向左平移
的图象向左平移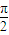 个单位.
个单位. 有如下性质:①函数是奇函数;②函数在
有如下性质:①函数是奇函数;②函数在 上是减函数,在
上是减函数,在 上是增函数.
上是增函数. (x>0)的值域是[6,+∞),求b的值;
(x>0)的值域是[6,+∞),求b的值; (常数c>0)在定义域内的奇偶性和单调性,并加以证明;
(常数c>0)在定义域内的奇偶性和单调性,并加以证明; (常数c>0)分别作出推广,使它们是你推广的函数的特例.判断推广后的函数的单调性(只需写出结论,不要证明).
(常数c>0)分别作出推广,使它们是你推广的函数的特例.判断推广后的函数的单调性(只需写出结论,不要证明).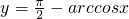 是奇函数;
是奇函数; 是sinA<cosB的充要条件;
是sinA<cosB的充要条件; -
- )的图象,只需将y=sin
)的图象,只需将y=sin 的图象向左平移
的图象向左平移 个单位.
个单位.| a |
| x |
| a |
| a |
| 2b |
| x |
| c |
| x2 |
| a |
| x |
| c |
| x2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com