
题目列表(包括答案和解析)
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AC⊥AD,AB⊥BC,∠BAC=45°,PA=AD=2,AC=1.
(Ⅰ)证明PC⊥AD;
(Ⅱ)求二面角A-PC-D的正弦值;
(Ⅲ)设E为棱PA上的点,满足异面直线BE与CD所成的角为30°,求AE的长.

【解析】解法一:如图,以点A为原点建立空间直角坐标系,依题意得A(0,0,0),D(2,0,0),C(0,1,0), 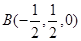 ,P(0,0,2).
,P(0,0,2).

(1)证明:易得 ,
, 于是
于是 ,所以
,所以
(2)  ,
, 设平面PCD的法向量
设平面PCD的法向量 ,
,
则 ,即
,即 .不防设
.不防设 ,可得
,可得 .可取平面PAC的法向量
.可取平面PAC的法向量 于是
于是 从而
从而 .
.
所以二面角A-PC-D的正弦值为 .
.
(3)设点E的坐标为(0,0,h),其中 ,由此得
,由此得 .
.
由 ,故
,故
所以, ,解得
,解得 ,即
,即 .
.
解法二:(1)证明:由 ,可得
,可得 ,又由
,又由 ,
, ,故
,故 .又
.又 ,所以
,所以 .
.

(2)如图,作 于点H,连接DH.由
于点H,连接DH.由 ,
, ,可得
,可得 .
.
因此 ,从而
,从而 为二面角A-PC-D的平面角.在
为二面角A-PC-D的平面角.在 中,
中, ,由此得
,由此得 由(1)知
由(1)知 ,故在
,故在 中,
中,
因此 所以二面角
所以二面角 的正弦值为
的正弦值为 .
.
(3)如图,因为 ,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故
,故过点B作CD的平行线必与线段AD相交,设交点为F,连接BE,EF. 故 或其补角为异面直线BE与CD所成的角.由于BF∥CD,故
或其补角为异面直线BE与CD所成的角.由于BF∥CD,故 .在
.在 中,
中, 故
故

在 中,由
中,由 ,
, ,
,
可得 .由余弦定理,
.由余弦定理, ,
,
所以 .
.
(请考生在题22,23,24中任选一题作答,如果多做,则按所做的第一题计分。)
(本小题满分10分)如图5,⊙O1和⊙O2公切线AD和BC相交于点D,A、B、C为切点,直线DO1与⊙O1与E、G两点,直线DO2交⊙O2与F、H两点。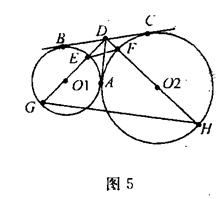
(1)求证: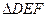 ~
~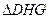 ;
;
(2)若⊙O1和⊙O2的半径之比为9:16,求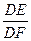 的值。
的值。
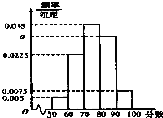 某培训班共有n名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示其中落在[80,90)内的频数为36.
某培训班共有n名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示其中落在[80,90)内的频数为36. (2006•南京一模)将三种作物种植在如图5块试验田里,每块种植一种作物,且同一种作物在相邻的试验田中,不同的种植方法有( )
(2006•南京一模)将三种作物种植在如图5块试验田里,每块种植一种作物,且同一种作物在相邻的试验田中,不同的种植方法有( ) 2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70)[70,75),[75,80),[80,85),[85,90)后得到如图5的频率分布直方图.
2012年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(km/t)分成六段:[60,65),[65,70)[70,75),[75,80),[80,85),[85,90)后得到如图5的频率分布直方图.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com