
题目列表(包括答案和解析)
如图,某隧道设计为双向四车道,车道总宽22米,要求通行车辆限高4.5米,隧道全长2.5千米,隧道的拱线近似地看成半个椭圆形状.

(Ⅰ)若最大拱高h为6米,则隧道设计的拱宽l是多少?
(Ⅱ)若最大拱高h不小于6米,则应如何设计拱高h和拱宽l,才能使半个椭圆形隧道的土方工程量最小?
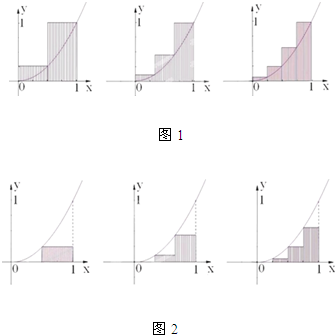
(半个椭圆的面积公式为S=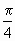 lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
lh,柱体体积为:底面积乘以高.本题结果均精确到0.1米)
 为了求函数y=x2,函数x=1,x轴围成的曲边三角形的面积S,古人想出了两种方案求其近似解(如图):第一次将区间[0,1]二等分,求出阴影部分矩形面积,记为S2;第二次将区间[0,1]三等分,求出阴影部分矩形面积,记为S3;第三次将区间[0,1]四等分,求出S4…依此类推,记图1中Sn=an,图2中Sn=bn,其中n≥2.
为了求函数y=x2,函数x=1,x轴围成的曲边三角形的面积S,古人想出了两种方案求其近似解(如图):第一次将区间[0,1]二等分,求出阴影部分矩形面积,记为S2;第二次将区间[0,1]三等分,求出阴影部分矩形面积,记为S3;第三次将区间[0,1]四等分,求出S4…依此类推,记图1中Sn=an,图2中Sn=bn,其中n≥2.| 1 |
| 3 |
| 1 |
| 6 |
(本题满分15分)如图,某机场建在一个海湾的半岛上,飞机跑道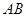 的长为4.5
的长为4.5 ,且跑道所在的直线与海岸线
,且跑道所在的直线与海岸线 的夹角为
的夹角为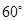 (海岸线可以看作是直线),跑道上离海岸线距离最近的点
(海岸线可以看作是直线),跑道上离海岸线距离最近的点 到海岸线的距离
到海岸线的距离 .
.
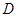 为海湾一侧海岸线
为海湾一侧海岸线 上的一点,设
上的一点,设 ,点
,点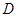 对跑道
对跑道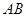 的视角为
的视角为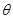 .
.
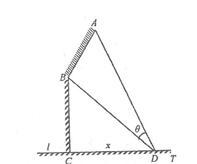
(1)
将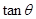 表示为
表示为 的函数;
的函数;
(2)已知常数 ,对于任意的
,对于任意的 ,
,
 ,等号成立当
,等号成立当
且仅当 ,求点
,求点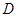 相对于垂足
相对于垂足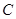 的位置,使
的位置,使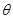 取得最大值.
取得最大值.
(本小题满分12分)
某校高三文科分为四个班.高三数学调研测试后, 随机地在各班抽取部分学生进行
测试成绩统计,各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人.
抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,其中120~130
(包括120分但不包括130分)的频率为0.05, 此分数段的人数为5人.
(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,
任取一名学生, 求分数
不小于90分的概率.

(本小题满分12分)[来源:学科网ZXXK]
某校高三文科分为四个班.高三数学调研测试后,
随机地在各班抽取部分学生进行测试成绩统计,
各班被抽取的学生人数恰好成等差数列,人数最少的班被抽取了22人。
抽取出来的所有学生的测试成绩统计结果的频率分布条形图如图5所示,
其中120~130(包括120分但不包括130分)的频率为0.05,此 0
分数段的人数为5人![]()

(1)问各班被抽取的学生人数各为多少人?
(2)在抽取的所有学生中,任取一名学生, 求分数不小(![]() 本小题满分12分)
本小题满分12分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com