
题目列表(包括答案和解析)

 (2013•未央区三模)某三棱锥的三视图如图所示,该三棱锥的体积是为( )
(2013•未央区三模)某三棱锥的三视图如图所示,该三棱锥的体积是为( )给出两个命题: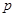 :
: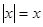 的充要条件是
的充要条件是 为非负实数;
为非负实数;
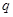 :奇函数的图像一定关于原点对称,则假命题是 ( )
:奇函数的图像一定关于原点对称,则假命题是 ( )
A.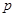 或
或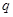 B.
B.
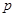 且
且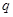 C.﹁
C.﹁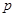 且
且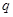 D.﹁
D.﹁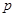 或
或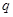
INPUT a,b
WHILE a<>b
IF a>=b THEN
a=a-b
ELSE
b=b-a
ENDIF
WEND
PRINT a
END
A.求a/b的余数 B.求a,b的最小公倍数
C.求a被b整除的商 D.求a,b的最大公约数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com