
题目列表(包括答案和解析)
解关于 的不等式
的不等式

【解析】本试题主要考查了含有参数的二次不等式的求解,
首先对于二次项系数a的情况分为三种情况来讨论,
A=0,a>0,a<0,然后结合二次函数的根的情况和图像与x轴的位置关系,得到不等式的解集。
解:①若a=0,则原不等式变为-2x+2<0即x>1
此时原不等式解集为 ;
; 
②若a>0,则ⅰ) 时,原不等式的解集为
时,原不等式的解集为 ;
;
ⅱ) 时,原不等式的解集为
时,原不等式的解集为 ;
;
ⅲ) 时,原不等式的解集为
时,原不等式的解集为 。
。 
③若a<0,则原不等式变为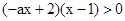
 原不等式的解集为
原不等式的解集为 。
。
设双曲线 的两个焦点分别为
的两个焦点分别为 、
、 ,离心率为2.
,离心率为2.
(1)求双曲线的渐近线方程;
(2)过点 能否作出直线
能否作出直线 ,使
,使 与双曲线
与双曲线 交于
交于 、
、 两点,且
两点,且 ,若存在,求出直线方程,若不存在,说明理由.
,若存在,求出直线方程,若不存在,说明理由.
【解析】(1)根据离心率先求出a2的值,然后令双曲线等于右侧的1为0,解此方程可得双曲线的渐近线方程.
(2)设直线l的方程为 ,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理
,然后直线方程与双曲线方程联立,消去y,得到关于x的一元二次方程,利用韦达定理 表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
表示此条件,得到关于k的方程,解出k的值,然后验证判别式是否大于零即可.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com