
题目列表(包括答案和解析)
解::因为![]() ,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=
,所以f(1)f(2)<0,因此f(x)在区间(1,2)上存在零点,又因为y=![]() 与y=-
与y=-![]() 在(0,+
在(0,+![]() )上都是增函数,因此
)上都是增函数,因此![]() 在(0,+
在(0,+![]() )上是增函数,所以零点个数只有一个方法2:把函数
)上是增函数,所以零点个数只有一个方法2:把函数![]() 的零点个数个数问题转化为判断方程
的零点个数个数问题转化为判断方程![]() 解的个数问题,近而转化成判断
解的个数问题,近而转化成判断![]() 与
与![]() 交点个数问题,在坐标系中画出图形
交点个数问题,在坐标系中画出图形
由图看出显然一个交点,因此函数![]() 的零点个数只有一个
的零点个数只有一个
袋中有50个大小相同的号牌,其中标着0号的有5个,标着n号的有n个(n=1,2,…9),现从袋中任取一球,求所取号码的分布列,以及取得号码为偶数的概率.
19C.解:由![]() 得
得![]() ,所以
,所以![]() ,所以
,所以 ,因为f(x)=x,所以
,因为f(x)=x,所以 解得x=-1或-2或2,所以选C
解得x=-1或-2或2,所以选C
调查某医院某段时间内婴儿出生时间与性别的关系,得到以下数据。
| 晚上 | 白天 | 合计 | |
| 男婴 | 24 | 31 | 55 |
| 女婴 | 8 | 26 | 34 |
| 合计 | 32 | 57 | 89 |
试问有多大把握认为婴儿的性别与出生时间有关系?
 得
得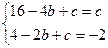 ,所以
,所以 ,所以
,所以 ,因为f(x)=x,所以
,因为f(x)=x,所以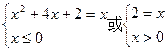 解得x=-1或-2或2,所以选C
解得x=-1或-2或2,所以选C| | 晚上 | 白天 | 合计 |
| 男婴 | 24 | 31 | 55 |
| 女婴 | 8 | 26 | 34 |
| 合计 | 32 | 57 | 89 |
已知Pn(an,bn)都在直线L:y=2x+2上,P1为直线L与x轴的交点,数列{an}成等差数列,公差为1(n∈N*)
(Ⅰ)求数列{an},{bn}的通项公式
(Ⅱ)若f(n)= 问是否存在k∈N*,使得f(k+5)=2f(k)-2成立,若存在,求出k的值;若不存在,说明理由.
问是否存在k∈N*,使得f(k+5)=2f(k)-2成立,若存在,求出k的值;若不存在,说明理由.
已知函数f(x)的定义域为D,且f(x)同时满足以下条件:
①f(x)在D上单调递增或单调递减;
②存在区间[a,b] D,使得f(x)在[a,b]上的值域是[a,b],那么我们把函数f(x)(x∈D)叫做闭函数.
D,使得f(x)在[a,b]上的值域是[a,b],那么我们把函数f(x)(x∈D)叫做闭函数.
(1)求闭函数y=-x3符合条件2的区间[a,b].
(2)判断函数y=2x-lgx是不是闭函数?若是,请说明理由,并找出区间[a,b];若不是,请说明理由.
(3)若y=k+ 是闭函数,求实数k的取值范围.
是闭函数,求实数k的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com