
题目列表(包括答案和解析)
| 1 | 8 |

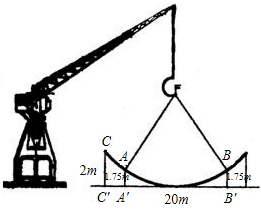 如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)
如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)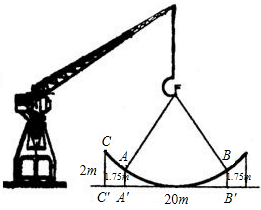 如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)
如图:是一抛物线型钢结构,钢结构CD的跨度为20米,拱高CC’=2米.假定用吊车从地面吊起,吊钩位于抛物线顶点O的正上方12.5米点F处,吊绳分别挂在距离地面1.75米的A、B两处,求吊绳的FA、FB的总长.(计算过程中可能用到以下参考数据:4.32=18.49,4.72=22.09,5.32=28.09,5.72=32.49)
| 1 |
| 10 |
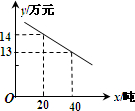 (2)根据题中条件和(1)的结果,求年利润w甲(万元)与x(吨)之间的函数关系式和甲的最大年利润;
(2)根据题中条件和(1)的结果,求年利润w甲(万元)与x(吨)之间的函数关系式和甲的最大年利润;| 1 |
| 10 |
| b |
| 2a |
| 4ac-b2 |
| 4a |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com