
题目列表(包括答案和解析)
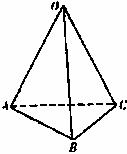
如图,在四面体O―ABC中,OA=OB=OC=1.![]() ∠AOB=∠AOC=
∠AOB=∠AOC=![]() ,则二面角
,则二面角
|
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
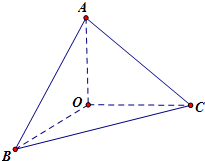 如图所示,三棱锥O-ABC中,OA=OB=OC=2,且,OA、OB、OC两两垂直(每两条都垂直).
如图所示,三棱锥O-ABC中,OA=OB=OC=2,且,OA、OB、OC两两垂直(每两条都垂直). 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设 ,二面角B-OA-C、
,二面角B-OA-C、 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为 ;
; ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为 ;
; 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;
 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设 ,二面角B-OA-C、
,二面角B-OA-C、 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为 ;
; ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为 ;
; 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;
 在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设
在球面上围成的部分叫做球面三角形,记作球面三角形ABC,在球面三角形ABC中,OA=1,设 ,二面角B-OA-C、
,二面角B-OA-C、 ,则球面三角形ABC的面积为
,则球面三角形ABC的面积为 ;
; ,则四面体OABC的侧面积为
,则四面体OABC的侧面积为 ;
; 在点A处的切线l1与圆弧
在点A处的切线l1与圆弧 在点A处的切线l2的夹角等于a;
在点A处的切线l2的夹角等于a;
一、选择题
|