
题目列表(包括答案和解析)
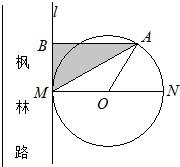 长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米)
长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米)设a,b为常数,![]() :把平面上任意一点
:把平面上任意一点
(a,b)映射为函数![]()
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当![]() ,这里t为常数;
,这里t为常数;
(3)对于属于M的一个固定值![]() ,得
,得![]() ,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象.
,在映射F的作用下,M1作为象,求其原象,并说明它是什么图象.
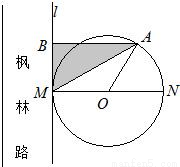
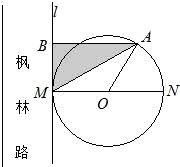 长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米)
长沙市将河西作为环境友好型和资源节约型的两型社会先导区,为加强先导区的建设,要改造枫林路,如图所示,规划沿路修建圆形休闲广场,圆心为O,半径为100米,其与枫林路一边所在的直线l相切于M点,A为上半圆弧上一点.过点A作l的垂线,垂足为B,市园林局计划在△ABM内进行绿化,设△ABM的面积为S(单位:平方米)设a,b为常数,M{f(x)|f(x)=acosx+bsinx};F:把平面上任意一点(a,b)映射为函数acodx+bsinx.
(1)证明:不存在两个不同点对应于同一个函数;
(2)证明:当f0(x)ÎM时,f1(x)=f0(x+t)ÎM,这里t为常数;
(3)对于属于M的一个固定值f0(x),得M1={f0(x+t),tÎR},在映射F的作用下,M1作为象,求其原象,并说明它是什么图像.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com