A.8　　　　　      B. 9       　         C. 10　　　　　    D.11

（07年湖南卷文）在的二项展开式中，若只有的系数最大，则

　 A．8　　　　　      B. 9       　         C. 10　　　　　    D.11

       ①终边相同的角的同名三角函数值相等　②终边不同的角的同名三角函数值不等　③若sinα＞0,则α是第一、二象限的角　④若α是第二象限的角,且P(x,y)是其终边上一点,则cosα=

    A.1　　　　B.2　　　　C.3　　　　D.4

一次函数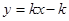，若y随x的增大而增大，则它的图象经过    （    ）

A.第一、二、三象限　　       B.第一、三、四象限　　

C.第一、二、四象限　　       D. 第二、三、四象限

在10件产品中有3件次品，从中选3件．下列各种情况是互斥事件的有(    )

①A: “所取3件中至多2件次品”， B : “所取3件中至少2件为次品”；

②A: “所取3件中有一件为次品”，B： “所取3件中有二件为次品”；

③A：“所取3件中全是正品”，B：“所取3件中至少有一件为次品”；

④A：“所取3件中至多有2件次品”，B：“所取3件中至少有一件是正品”；

A．①③　　　B．②③　　　C．②④　　　D．③④