
题目列表(包括答案和解析)
| A、5次 | B、6次 | C、7次 | D、8次 |
| x-a |
| x-b |
| x2-2x |
| x-1 |
若角A是第二象限角,则角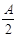 是第几象限角
是第几象限角
A.一或三 B.二或四 C.三或四 D.一或四
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140.150] |
| 频数 | 1 | 2 | 12 | 13 | 12 | 9 | 1 | 0 |
| 分组 | [70,80) | [80,90) | [90,100) | [100,110) | [110,120) | [120,130) | [130,140) | [140.150] |
| 频数 | 2 | 3 | 13 | 11 | 9 | 10 | 1 | 1 |
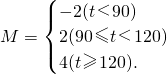 ,分别求这两个班学生数学成绩的M总值,并据此对这两个班数学成绩总体水平作一简单评价.
,分别求这两个班学生数学成绩的M总值,并据此对这两个班数学成绩总体水平作一简单评价.方程![]() 表示焦点在坐标轴上的双曲线,则α是第几象限的角( )
表示焦点在坐标轴上的双曲线,则α是第几象限的角( )
A.二 B.四 C.二或四? D.一或三
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com