
题目列表(包括答案和解析)
有一定质量的二氧化碳,当它的体积V=5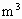 时,它的密度r
=1.98kg/
时,它的密度r
=1.98kg/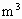 (注:质量、体积、密度之间的关系为
(注:质量、体积、密度之间的关系为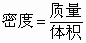 ).
).
(1)求r 与V的函数关系式;
(2)要使密度不低于1.5kg/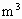 ,则需要的容器体积最大是多少立方米?
,则需要的容器体积最大是多少立方米?
有一定质量的二氧化碳,当它的体积V=5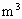 时,它的密度r
=1.98kg/
时,它的密度r
=1.98kg/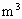 (注:质量、体积、密度之间的关系为
(注:质量、体积、密度之间的关系为 ).
).
(1)求r 与V的函数关系式;
(2)要使密度不低于1.5kg/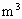 ,则需要的容器体积最大是多少立方米?
,则需要的容器体积最大是多少立方米?
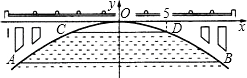 上升3米,则水面CD的宽是10米.
上升3米,则水面CD的宽是10米.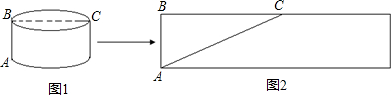
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com