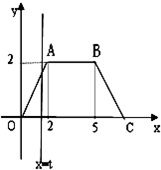如图，在等腰梯形OABC中，A（2，2），B（5，2）．直线x=t（t＞0）由点O向点C移动，至点C完毕，记扫描梯形时所得直线x=t左侧的图形面积为f（t）．试求f（t）的解析式，并画出y=f（t）的图象．

查看答案和解析>>

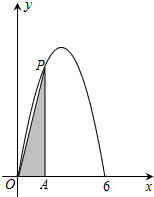已知函数f（x）=ax²+bx+c，x∈[0，6]的图象经过（0，0）和（6，0）两点，如图所示，且函数f（x）的值域为[0，9]．过动点P（t，f（t））作x轴的垂线，垂足为A，连接OP．
（I）求函数f（x）的解析式；
（Ⅱ）记△OAP的面积为S，求S的最大值．

查看答案和解析>>

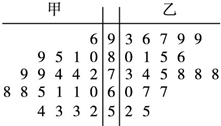某中学将100名高一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了解教学效果，期末考试后，陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计，作出茎叶图如下．记成绩不低于90分者为“成绩优秀”．
（Ⅰ）在乙班样本的20个个体中，从不低于86分的成绩中随机抽取2个，求抽出的两个均“成绩优秀”的概率；
（Ⅱ）由以上统计数据填写下面列联表，并判断是否有90%的把握认为：“成绩优秀”与教学方式有关．
附：K²=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

（此公式也可写成x²=

n(n11 n22-n12n21)2

n1+ n2+n+1n+2

）

P（k2≥K）	0.25	0.15	0.10	0.05	0.025
k	1.323	2.072	2.706	3.841	5.024

查看答案和解析>>

某中学将100名髙一新生分成水平相同的甲、乙两个“平行班”，每班50人．陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验．为了解教学效果，期末考试后，陈老师对甲、乙两个班级的学生成绩进行统计分析，画出频率分布直方图（如图）．记成绩不低于90分者为“成绩优秀”．

（Ⅰ）从乙班随机抽取2名学生的成绩，记“成绩优秀”的个数为ξ，求ξ的分布列和数学期望；
（Ⅱ）根据频率分布直方图填写下面2×2列联表，并判断是否有95%的把握认为：“成绩优秀”与教学方式有关．

	甲班（A方式）	乙班（B方式）	总计
成绩优秀
成绩不优秀
总计

附：K²=

n(ad-bc)2

(a+b)(c+d)(a+c)(b+d)

（此公式也可写成x²=

n(n11n22-n12n21)2

n1+n2+n+1n+2

）

查看答案和解析>>

查看答案和解析>>

一、选择题

1. D

解析:∵a₃+a₇+a₁₁=3a₇为常数，

∴S₁₃==13a₇，也是常数.

2. C

解析:∵易知q≠1,S₆∶S₃=1∶2=,q³=-,

∴S₉∶S₃==1+q³+q⁶=1-+(-)²=.

3．A ，

又

4．D  数列是以2为首项，以为公比的等比数列，项数为故选D。

5.B

6. D

解析:当q=1时，S_n,S_n+1,S_n+2构成等差数列；

当q=-2时，S_n+1,S_n,S_n+2构成等差数列；

当q=-时，S_n,S_n+2,S_n+1构成等差数列.

７．A   仅②不需要分情况讨论，即不需要用条件语句

8. D

9. D

解析:易知a_n=

∴a₁³+a₂³+…+a_n³=2³+8¹+8²+…+8^n-1=8+=(8^n-1+6).

10.A提示：依题意可得.

１１．B，指输入的数据．

１２．D 

（法一）辗转相除法：         

∴是和的最大公约数．

（法二）更相减损术：

        ∴是和的最大公约数．

二、填空题

13.

14.

当时，是正整数。

15.

解析:b_n===a₁,b_n+1=a₁,=(常数).

16．-6

三、解答题

17．解（1）

      以3为公比的等比数列.

 （2）由（1）知，..

      不适合上式，

       .

18．解：（1）a_n=    （2）.

19．解：(1)，；

（2）由（1）得，假设数列{b_n}中存在三项b_p,b_q,b_r(p,q,r互不相等)成等比数列，则 即

∴，，，得

∴p=r，矛盾.  ∴数列{b_n}中任意三项都不可能成等比数列.

20.解：设未赠礼品时的销售量为a₀个，而赠送礼品价值n元时销售量为a_n个，

，

又设销售利润为数列，

当，

考察的单调性，

当n=9或10时，最大

答：礼品价值为9元或10元时商品获得最大利润.

21.解析：（1）时，

即

两式相减：

即故有

。

数列为首项公比的等比数列。

（2）

则

又

（3）

   ①

而   ②

①-②得：

22.解：（1）b₄=b₁＋3d  即11=2＋3d， ∴b₁=2, b₂=5, b₃=8, b₄=11, b₅=8, b₆=5, b₇=2；

（2）S=C₁＋C₂＋…＋C₄₉=2(C₂₅＋C₂₆＋…＋C₄₉)－C₂₅=；

（3）,d₁₀₀=2＋3×49=149，∴d₁, d₂,…d₅₀是首项为149，公差为－3的等差数列.  

当n≤50时，

当51≤n≤100时,S_n=d₁＋d₂＋…d₅₀=S₅₀＋(d₅₁＋d₅₂＋…d_n)

                   =3775＋(n－50)×2＋=

∴综上所述,.

w.w.w.k.s.5.u.c.o.m