
题目列表(包括答案和解析)
鲁迅先生在论证“作文没有秘诀”时叙述:若作文有秘诀,则有许多祖传作家,因不存在许多祖传作家,所以作文没有秘诀.这里鲁迅先生说明“作文没有秘诀”运用了
综合法
分析法
反证法
以上都不是
鲁迅先生在论证“作文没有秘诀”时叙述:若作文有秘诀,则有许多祖传作家,因不存在许多祖传作家,所以作文没有秘诀.这里鲁迅先生说明“作文没有秘诀”运用了
综合法
分析法
反证法
以上都不是
解关于 的不等式:
的不等式:

【解析】解:当 时,原不等式可变为
时,原不等式可变为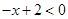 ,即
,即 (2分)
(2分)
当 时,原不等式可变为
时,原不等式可变为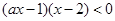
 (5分) 若
(5分) 若 时,
时, 的解为
的解为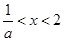 (7分)
(7分)
若 时,
时, 的解为
的解为 (9分) 若
(9分) 若 时,
时, 无解(10分) 若
无解(10分) 若 时,
时, 的解为
的解为 (12分综上所述
(12分综上所述
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为
时,原不等式的解为
当 时,原不等式的解为:
时,原不等式的解为: 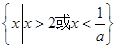
完成下列反证法证题的全过程:已知0<a≤3,函数f(x)=x3-ax在区间[1,+∞)上是增函数,设当x0≥1,f(x0)≥1时,有f(f(x0))=x0,求证:f(x0)=x0.
证明:假设f(x0)≠x0,则必有 ① 或 ② .
若 ③ ,由f(x)在区间[1,+∞)上是增函数,则f(f(x0))>f(x0).
又f(f(x0))=x0,所以f(x0)<x0,这与 ④ 矛盾.
若x0>f(x0)≥1,由f(x)在区间[1,+∞)上是增函数,则 ⑤ .
又f(f(x0))=x0,所以f(x0)>x0,这与 ⑥ 矛盾.
综上所述,当x0≥1,f(x0)≥1且f(f(x0))=x0时,有f(x0)=x0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com