已知函数f(x)=e^x-ax，其中a＞0.

（1）若对一切x∈R，f(x) 1恒成立，求a的取值集合；

（2)在函数f(x)的图像上去定点A（x₁, f(x₁)）,B(x₂, f(x₂))(x₁<x₂)，记直线AB的斜率为k，证明：存在x₀∈（x₁,x₂）,使恒成立.

【解析】解：令.

当时单调递减；当时单调递增，故当时，取最小值

于是对一切恒成立，当且仅当.　　　　　　　　①

令则

当时，单调递增；当时，单调递减.

故当时，取最大值.因此，当且仅当时，①式成立.

综上所述，的取值集合为.

（Ⅱ）由题意知，令则

令，则.当时，单调递减；当时，单调递增.故当，即

从而，又

所以因为函数在区间上的图像是连续不断的一条曲线，所以存在使即成立.

【点评】本题考查利用导函数研究函数单调性、最值、不等式恒成立问题等，考查运算能力，考查分类讨论思想、函数与方程思想等数学方法.第一问利用导函数法求出取最小值对一切x∈R，f(x) 1恒成立转化为从而得出求a的取值集合；第二问在假设存在的情况下进行推理，然后把问题归结为一个方程是否存在解的问题，通过构造函数，研究这个函数的性质进行分析判断.

已知函数f(x)＝alnx＋bx,且f(1)＝ －1，f′(1)＝0，

⑴求f(x)；

⑵求f(x)的最大值；

⑶若x＞0,y＞0,证明：lnx＋lny≤.

本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题，同时考查考生用函数放缩的方法证明不等式的能力．

A.

【命题意图】本题考查导数的概念与几何意义，中等题.

已知抛物线C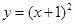：与圆有一个公共点A，且在A处两曲线的切线与同一直线l

（I）     求r；

（II）   设m、n是异于l且与C及M都相切的两条直线，m、n的交点为D，求D到l的距离。

【解析】本试题考查了抛物线与圆的方程，以及两个曲线的公共点处的切线的运用，并在此基础上求解点到直线的距离。

【点评】该试题出题的角度不同于平常，因为涉及的是两个二次曲线的交点问题，并且要研究两曲线在公共点出的切线，把解析几何和导数的工具性结合起来，是该试题的创新处。另外对于在第二问中更是难度加大了，出现了另外的两条公共的切线，这样的问题对于我们以后的学习也是一个需要练习的方向。

已知函数

（I）     讨论f（x）的单调性；

（II）   设f（x）有两个极值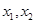点若过两点的直线I与x轴的交点在曲线上，求α的值。

【解析】本试题考查了导数在研究函数中的运用。第一就是三次函数，通过求解导数，求解单调区间。另外就是运用极值的概念，求解参数值的运用。

【点评】试题分为两问，题面比较简单，给出的函数比较常规，，这一点对于同学们来说没有难度但是解决的关键还是要看导数的符号的实质不变，求解单调区间。第二问中，运用极值的问题，和直线方程的知识求解交点，得到参数的值。

（1）