
题目列表(包括答案和解析)
(本小题考查函数定义域的概念及综合知识的应用 )
函数 的定义域为
的定义域为
A. B
B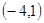 C
C D
D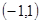 。
。
设二项式
 的展开式中第7项的系数与倒数第7项的系数之比是
的展开式中第7项的系数与倒数第7项的系数之比是 .
.
(Ⅰ)求 ;
;
(Ⅱ)展开式中有多少项的系数是有理数,指出它们分别是哪几项.
本题考查二项式定理、二项式系数与系数的概念、二项式定理的通项的应用,属基本题
(本小题考查函数定义域的概念及综合知识的应用 )
函数![]() 的定义域为
的定义域为
A. ![]() B
B![]() C
C![]() D
D![]() 。
。
已知A(—2,4)、B(3,—1)、C(—3,—4)且![]() ,
,![]() ,求点M、N的坐标及向量
,求点M、N的坐标及向量![]() 的坐标.
的坐标.
[解题思路]: 利用平面向量的基本本概念及其坐标表示求解。
在复平面内,  是原点,向量
是原点,向量 对应的复数是
对应的复数是 ,
, =2+i。
=2+i。
(Ⅰ)如果点A关于实轴的对称点为点B,求向量 对应的复数
对应的复数 和
和 ;
;
(Ⅱ)复数 ,
, 对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
对应的点C,D。试判断A、B、C、D四点是否在同一个圆上?并证明你的结论。
【解析】第一问中利用复数的概念可知得到由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i ∵
=-2i ∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
=
第二问中,由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
(Ⅰ)由题意得,A(2,1) ∴B(2,-1)
∴  =(0,-2)
∴
=(0,-2)
∴ =-2i 3分
=-2i 3分
∵  (2+i)(-2i)=2-4i,
∴
(2+i)(-2i)=2-4i,
∴  =
= 2分
2分
(Ⅱ)A、B、C、D四点在同一个圆上。 2分
证明:由题意得, =(2,1)
∴
=(2,1)
∴
同理 ,所以A、B、C、D四点到原点O的距离相等,
,所以A、B、C、D四点到原点O的距离相等,
∴A、B、C、D四点在以O为圆心, 为半径的圆上
为半径的圆上
一、选择题
1.B 2.A 3.C 4.C 5.A6.D 7.C10.B11.C
w.w.w.k.s.5.u.c.o.m

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com