
题目列表(包括答案和解析)
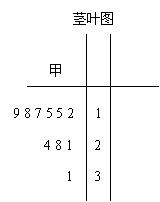 (本题10分)某校在参加ZSBL“动感地带”浙江省第四届中学生篮球联赛竞赛前,欲再从甲、乙两人中挑选一人参赛,已知赛前甲最近参加的十场比赛得分如下茎叶图所示,赛前乙最近参加的十场比赛得分分别为20、15、12、29、14、16、17、22、25、30,
(本题10分)某校在参加ZSBL“动感地带”浙江省第四届中学生篮球联赛竞赛前,欲再从甲、乙两人中挑选一人参赛,已知赛前甲最近参加的十场比赛得分如下茎叶图所示,赛前乙最近参加的十场比赛得分分别为20、15、12、29、14、16、17、22、25、30,
请回答:
(1)甲近十场比赛得分的极差、众数、中位数分别是多少?
(2)甲近十场比赛得分在![]() 间的频率是多少?
间的频率是多少?
(3)应选派谁参加更合理?
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):

 男 女
男 女
 15
7 7 8 9 9 9
15
7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
(本小题满分12分)
第8届中学生模拟联合国大会将在本校举行,为了搞好接待工作,组委会招募了12名男志愿者和18名女志愿者.将这30名志愿者的身高编成如下茎叶图(单位:cm):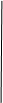
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9
9 8 16 0 0 1 2 4 5 8 9
8 6 5 0 17 2 5 6
7 4 2 1 18 0
1 0 19
若男生身高在180cm以上(包括180cm)定义为“高个子”, 在180cm以下(不包括180cm)定义为“非高个子”, 女生身高在170cm以上(包括170cm)定义为“高个子”,在170cm以下(不包括170cm)定义为“非高个子”.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中抽取6人,则应分别抽取“高个子”、“非高个子”各几人?
(2)从(1)中抽出的6人中选2人担任领座员,那么至少有一人是“高个子”的概率是多少?
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9. 为了了解我校今年准备报考飞行员的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,第2小组的频数为12,则报考飞行员的学生人数是 .

第15题图 第16题图
 一、选择题
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
C
A
A
D
C
B
A
D
B
B
二、填空题
13. 14.
14.  15.7500 16.
15.7500 16.
三、解答题
17.证明:(Ⅰ)取AB的中点M,连FM,MC, ┅┅┅┅2分
∴ FM∥EB, FM= EB=CD, ┅┅┅┅┅┅┅4分
EB=CD, ┅┅┅┅┅┅┅4分
∵ EB、CD都垂直于平面ABC
∴ CD∥BE∴ CD∥FM,
∴四边形FMCD是平行四边形,
∴ FD∥MC.又∵
∴FD∥平面ABC ┅┅┅┅┅┅┅6分
(Ⅱ)∵M是AB的中点,CA=CB,
∴CM⊥AB, ┅┅┅┅┅┅┅8分
又 CM⊥BE, ∴CM⊥面EAB, ∴CM⊥BF, ∴FD⊥BF, ┅┅┅┅┅┅┅10分
∵F是AE的中点, EB=AB∴BF⊥EA. ∴BF⊥平面ADE ┅┅┅┅┅┅┅12分
18解:
(Ⅰ)实数对 有
有
 共16种不同的情况,有16条不同的直线.┅┅┅┅┅┅┅4分
共16种不同的情况,有16条不同的直线.┅┅┅┅┅┅┅4分
当实数对 为
为 时,直线
时,直线 的斜率
的斜率 ,直线倾斜角大于
,直线倾斜角大于 ,
,
所以直线 倾斜角大于
倾斜角大于 的概率为
的概率为 ;┅┅┅┅┅┅┅6分
;┅┅┅┅┅┅┅6分
(Ⅱ)直线 在x轴上的截距与在y轴上截距之差
在x轴上的截距与在y轴上截距之差 ,即
,即 ,┅┅┅┅┅┅┅8分
,┅┅┅┅┅┅┅8分
当实数对 为
为 时
时 ,┅┅┅┅┅┅┅10分
,┅┅┅┅┅┅┅10分
所以直线 在x轴上的截距与在y轴上截距之差小于7的概率为
在x轴上的截距与在y轴上截距之差小于7的概率为 . ┅┅┅┅12分
. ┅┅┅┅12分
19解:(1)

┅┅┅┅┅┅┅4分
因为 ,所以
,所以 ,所以
,所以 ,
,
 即
即 的取值范围为
的取值范围为 ┅┅┅┅┅┅┅6分
┅┅┅┅┅┅┅6分
(Ⅱ)因为 ,所以
,所以 ┅┅┅┅┅┅┅8分
┅┅┅┅┅┅┅8分

所以 的最小值为
的最小值为 ,当
,当 即
即 为等边三角形时取到. ┅┅┅┅┅┅┅12分
为等边三角形时取到. ┅┅┅┅┅┅┅12分
20解:(Ⅰ) 的首项为
的首项为 ,所以
,所以 ┅┅┅┅┅┅┅3分
┅┅┅┅┅┅┅3分
所以 ,所以
,所以 是等差数列,首项为
是等差数列,首项为 ,公差为1
,公差为1
┅┅┅┅┅┅┅6分
(Ⅱ)由(Ⅰ)可得 ,即
,即 ┅┅┅┅┅┅┅7分
┅┅┅┅┅┅┅7分
令 ①
①
则 ②┅┅┅┅┅┅9分
②┅┅┅┅┅┅9分
①-②可得
所以 ,所以
,所以 ┅┅12分
┅┅12分
21解:(Ⅰ)由题意可知,可行域是以 及点
及点 为顶点的三角形,∵
为顶点的三角形,∵ ,∴
,∴ 为直角三角形,
┅┅┅┅┅┅┅2分
为直角三角形,
┅┅┅┅┅┅┅2分
∴外接圆C以原点O为圆心,线段A .
.
∵ ,可得
,可得 .
.
∴所求圆C与椭圆C1的方程分别是 和
和 . ┅┅┅┅┅┅┅4分
. ┅┅┅┅┅┅┅4分
(Ⅱ2) F ,设
,设 ,,
,,
当 时,Q点为(
时,Q点为( ),可得
),可得 ,∴PF
,∴PF OQ.
OQ.
当 时,
时, ,可以解得
,可以解得 ,也有PF
,也有PF OQ. ┅┅┅6分
OQ. ┅┅┅6分
当 且
且
 时,OP的斜率为
时,OP的斜率为 ,则切线PQ的斜率为
,则切线PQ的斜率为 ,则PQ的方程为:
,则PQ的方程为: 化简为:
化简为: ,
┅┅┅8分
,
┅┅┅8分
 与
与 交得Q点坐标为
交得Q点坐标为 ┅┅┅10分
┅┅┅10分
则 ,
,



∴PF OQ.
OQ.
综上,直线PF与直线OQ垂直. ┅┅┅12分
22解:(Ⅰ) ┅┅┅┅┅┅┅2分
┅┅┅┅┅┅┅2分
①当 ,即
,即 ,在R上有
,在R上有 ,所以
,所以 在R单调递增;┅┅┅┅┅┅┅4分
在R单调递增;┅┅┅┅┅┅┅4分
②当 ,即
,即 ,当
,当 时,在
时,在 上有
上有 ,所以
,所以 在R单调递增;当
在R单调递增;当 时,在
时,在 上有
上有 ,所以
,所以 在R单调递增;┅┅┅┅┅┅┅6分
在R单调递增;┅┅┅┅┅┅┅6分
③当 ,即
,即
 两个根分别为,所以在
两个根分别为,所以在 上有
上有 ,即
,即 在
在 单调递增;
单调递增;
在 上有
上有 ,即
,即 在
在 单调递减.┅┅┅┅┅┅┅8分
单调递减.┅┅┅┅┅┅┅8分
(Ⅱ)由(Ⅰ)可知当 时函数
时函数 有极值,
有极值,
当 时,
时, ,所以不符合题意.
,所以不符合题意.
当 时,
时, ,此时函数
,此时函数 的极值点都为正数
的极值点都为正数
┅┅┅┅┅┅┅10分
 有极大值
有极大值 ,极小值
,极小值 ,所以
,所以
 ,
,
又因为 ,
,
所以
= ,┅┅┅┅┅┅┅12分
,┅┅┅┅┅┅┅12分
令 ,则
,则 ,所以
,所以 时
时 单调递增,所以
单调递增,所以 ,即
,即 极值之和小于
极值之和小于 . ┅┅┅┅┅┅┅14分
. ┅┅┅┅┅┅┅14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com