已知四棱锥P-ABCD，底面ABCD是∠A=60°、边长为a的菱形，又PD⊥底ABCD，且PD=CD，点M、N分别是棱AD、PC的中点．
（1）证明：DN∥平面PMB；
（2）证明：平面PMB⊥平面PAD；
（3）求点A到平面PMB的距离．

查看答案和解析>>

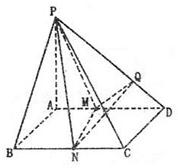已知四棱锥P-ABCD（如图），底面是边长为2的正方形，侧棱PA⊥底面ABCD，M、N分别为AD、BC的中点，MQ⊥PD于Q．
（1）求证：平面PMN⊥平面PAD；
（2）PA=2，求PM与平面PCD所成角的正弦值；
（3）求二面角P-MN-Q的余弦值．

查看答案和解析>>

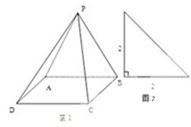已知四棱锥P-ABCD的直观图（如图1）及左视图（如图2），底面ABCD是边长为2的正方形，平面PAB⊥平面ABCD，PA=PB．
（Ⅰ）求证：AD⊥PB；
（Ⅱ）求异面直线PD与AB所成角的余弦值；
（Ⅲ）求平面PAB与平面PCD所成锐二面角的大小．

查看答案和解析>>

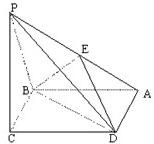已知四棱锥P-ABCD的底面是边长为a的菱形，∠ABC=120°，又PC⊥平面ABCD，PC=a，E是PA的中点．
（1）求证：平面EBD⊥平面ABCD；
（2）求直线PB与直线DE所成的角的余弦值；
（3）设二面角A-BE-D的平面角为θ，求cosθ的值．

查看答案和解析>>

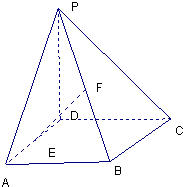已知四棱锥P-ABCD的底面ABCD是边长为1的正方形，PD⊥底面ABCD，PD=AD．
（1）求证：BC∥平面PAD；
（2）若E、F分别为PB、AD的中点，求证：EF⊥BC；
（3）求二面角C-PA-D的余弦值．

查看答案和解析>>

一、选择题

1、B      

2、A    

3、D  ④少了“”这个条件，其余3个是正确的。

4、B      

5、C  取AC的中点O，则  四面体ABCD外接球的球心为O，半径为 

6、D  设

7、D  由题意知，P点的轨迹为抛物线，以AB的中点为原点，AB所在直线为轴或轴可得四个标准方程

8、A 

9、A  ，1，－1是方程的两根

10、C  若无最小值

当  有最小值等价于

有大于0的最小值，即

11、C      

  直线AB的斜率为1

当过C点的切线与AB平行时，面积取最大值设此直线方程为

  C到AB距离为

12、C  的整数解为

这8个点两两所连的不过原点的直线有24条，过这8个点的切线有8条，每条直线确定了唯一的有序数对,共有32条。

二、填空题

13、 

14、    取AD中点E，连  为菱形，且

在侧面

上的投影，为所求，

15、 0  

又为偶函数 

16、 ②④   ①错  ②对

 ③错 

 当且仅当取等号  ④对

三、解答题

17、（1）

  即时 有最大值

（2）

18、（1）该爱好者得2分的概率为

（2）答对题的个数为，得分为，的可能取值为0，2，4，8

的分布列为

0

2

4

8

P

的数学期望为

以D为原点，DA、DC、DP分别为轴建系如图，

则

19、（1）       

由  知为平面PAD的一个法向量

又    

（2） 

（3）由（1）知为平面的一个法向量，

设平面的法向量为

令

 即二面角的余弦值为

20、（1）

 当   当

上单增

处取得极小值

的最大值为  最小值为

（2）由（1）知当

故对任意

只要对任意恒成立，即恒成立

记    

实数的取值范围是

21、（1）

  当

不是等比数列，当时， 数列是等比数列

且公比为2，

（2）由（1）知当

 1°

  2°

1°－2°及－

即

22、（1）设椭圆C的方程为

椭圆C的方程为

（2）由

  设与椭圆C交点为

将

①

则

消去得 

即    

  由①得

综上所述