
题目列表(包括答案和解析)
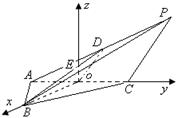
如图,在三棱锥![]() 中,
中,![]() 是正三角形,
是正三角形,![]() ,D是
,D是![]() 的中点,二面角
的中点,二面角![]() 为120,
为120,![]() ,
,![]() .取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
.取AC的中点O为坐标原点建立空间直角坐标系,如图所示,BD交z轴于点E.
(I)求B、D、P三点的坐标;
(II)求异面直线AB与PC所成的角;
已知正方体ABCD-A1B1C1D1,
O是底面ABCD对角线的交点.
(1)求证:A1C⊥平面AB1D1;
(2)求 .
.

【解析】(1)证明线面垂直,需要证明直线垂直这个平面内的两条相交直线,本题只需证: 即可.
即可.
(2)可以利用向量法,也可以根据平面A1ACC1与平面AB1D1垂直,可知取B1D1的中点E,则 就是直线AC与平面AB1D1所成的角.然后解三角形即可.
就是直线AC与平面AB1D1所成的角.然后解三角形即可.

A.45° B.90° C.60° D.不能确定
在正方体AC1中, M为棱DD1的中点, O为底面ABCD的中心, P为棱A1B1上任意一点, 则直线OP与AM所成的角为 ( )
A.30° B.60° C.90° D.120°
(12分)
学校欲在操场边上一直角三角形空地ABC上种植草坪,并需铺设一根水管EF(E在AC上,F在AB上)用于灌溉,已知∠A=30°,∠C=90°,BC=2a,D是BC中点,为确保灌溉的效果,铺设时要求∠EDF=60°。现有两种方案可供参考。甲方案:取AC的中点E铺设水管;乙方案:取AB的中点F铺设水管。

(1)比较甲乙两种方案,哪一种方案更合理(EF的长较小的合理);
(2)学校研究小组通过研究得出:无论D在BC的什么位置,总存在E,F两点,使△DEF为正三角形。试证明该结论的正确性。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com