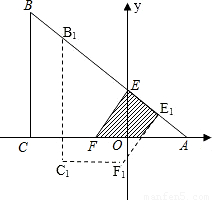
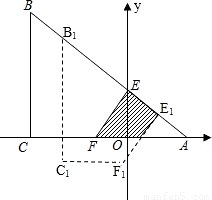
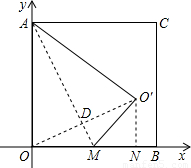
(2008•荆州)如图,等腰直角三角形纸片ABC中,AC=BC=4,∠ACB=90°,直角边AC在x轴上,B点在第二象限,A(1,0),AB交y轴于E,将纸片过E点折叠使BE与EA所在直线重合,得到折痕EF(F在x轴上),再展开还原沿EF剪开得到四边形BCFE,然后把四边形BCFE从E点开始沿射线EA平移,至B点到达A点停止.设平移时间为t(s),移动速度为每秒1个单位长度,平移中四边形BCFE与△AEF重叠的面积为S.
(1)求折痕EF的长;
(2)是否存在某一时刻t使平移中直角顶点C经过抛物线y=x
2+4x+3的顶点?若存在,求出t值;若不存在,请说明理由;
(3)直接写出S与t的函数关系式及自变量t的取值范围.