
题目列表(包括答案和解析)
| 最后二次射击总成绩 | 第8次射击需得成绩 |
| 20环 | ______ |
| 19环 | ______ |
| 18环 | ______ |
生活中,在分析研究比赛成绩时经常要考虑不等关系.例如:一射击运动员在一次比赛中将进行10次射击,已知前7次射击共中61环,如果他要打破88环(每次射击以1到10的整数环计数)的记录,问第8次射击不能少于多少环?
我们可以按以下思路分析:
首先根据最后二次射击的总成绩可能出现的情况,来确定要打破88环的记录,第8次射击需要得到的成绩,并完成下表:
| 最后二次射击总成绩 | 第8次射击需得成绩 |
| 20环 | |
| 19环 | |
| 18环 |
根据以上分析可得如下解答:
解:设第8次射击的成绩为x环,则可列出一个关于x的不等式:
_______________________________________
解得 _______________
所以第8次设计不能少于________环.
读理解下列例题,再完成练习.
例题:解不等式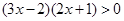
解:由有理数的乘法方法可知“两数相乘,同号得正”,因此可得
①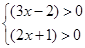 ②
②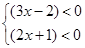
解不等式组①得 解不等式组②得
解不等式组②得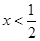
所以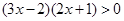 的解集
的解集 或
或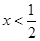 (2)
(2)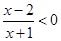
读理解下列例题,再完成练习.
例题:解不等式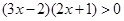
解:由有理数的乘法方法可知“两数相乘,同号得正”,因此可得
①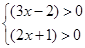 ②
②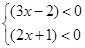
解不等式组①得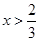 解不等式组②得
解不等式组②得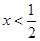
所以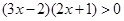 的解集
的解集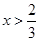 或
或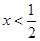 (2)
(2)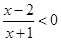
 .解:当
.解:当 时,原方程可化为
时,原方程可化为 ,解得
,解得 ;当
;当 时,原方程可化为
时,原方程可化为 ,解得
,解得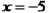 .所以原方程的解是
.所以原方程的解是 或
或

 为何值时,关于
为何值时,关于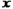 的方程
的方程 ⑴无解;⑵只有一个解;⑶有两个解
⑴无解;⑵只有一个解;⑶有两个解湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com