
题目列表(包括答案和解析)
2012年5月,甘肃省岷县发生雹洪灾害,一批武警官兵奉命营救小山两侧A、B两地的被困人员,为了圆满完成空降任务,需知道小山高度及A、B两地的距离。已知当飞机飞至高空C处时,发现飞机与山顶P及村庄B在同一条直线上,且点A、B、C、P在同一平面内,
并测得A、B两地的俯角分别为75°和30°,飞机离A地的 距离AC=700(1+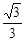 )米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).
)米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).
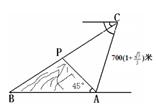
【解析】首先过点A作AE⊥BC于E,过点C作CF⊥AB于F,根据题意得:∠DCA=75°,∠DCB=30°,DC∥AB,然后由三角函数的知识,即可求得AE与EC的值,继而求得AB的值与小山的高
2012年5月,甘肃省岷县发生雹洪灾害,一批武警官兵奉命营救小山两侧A、B两地的被困人员,为了圆满完成空降任务,需知道小山高度及A、B两地的距离。已知当飞机飞至高空C处时,发现飞机与山顶P及村庄B在同一条直线上,且点A、B、C、P在同一平面内,
并测得A、B两地的俯角分别为75°和30°,飞机离A地的 距离AC=700(1+![]() )米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).
)米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).
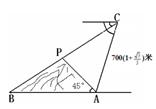
【解析】首先过点A作AE⊥BC于E,过点C作CF⊥AB于F,根据题意得:∠DCA=75°,∠DCB=30°,DC∥AB,然后由三角函数的知识,即可求得AE与EC的值,继而求得AB的值与小山的高
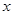 轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与
轴的垂线,垂足为A,连结OB,将△OAB沿OB折叠,使点A落在点A′处,A′B与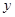 轴交于点F.
轴交于点F.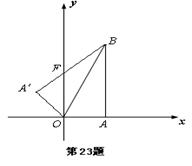
【答案】14![]() 。
。
【考点】轴对称-最短路线问题;勾股定理;垂径定理.
【专题】探究型.
【分析】先由MN=20求出⊙O的半径,再连接OA、OB,由勾股定理得出OD、OC的长,作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,在Rt△AB′E中利用勾股定理即可求出AB′的值.
【解答】∵MN=20,
∴⊙O的半径=10,
连接OA、OB,
在Rt△OBD中,OB=10,BD=6,
∴OD=![]() =
=![]() =8;
=8;
同理,在Rt△AOC中,OA=10,AC=8,
∴OC=![]() =
=![]() =6,
=6,
∴CD=8+6=14,
作点B关于MN的对称点B′,连接AB′,则AB′即为PA+PB的最小值,B′D=BD=6,过点B′作AC的垂线,交AC的延长线于点E,
在Rt△AB′E中,
∵AE=AC+CE=8+6=14,B′E=CD=14,
∴AB′=![]() =
=![]() =14
=14![]() .
.
故答案为:14![]() .
.
【点评】本题考查的是轴对称-最短路线问题、垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.
如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点c.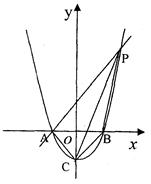
【小题1】(1)求A、B、C三点的坐标.
【小题2】(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
【小题3】 (3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似.若存在,请求出M点的坐标;否则,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com