
题目列表(包括答案和解析)
【答案】x≥1。
【考点】二次根式有意义的条件.
【专题】存在型.
【分析】先根据二次根式有意义的条件列出关于x的不等式,求出x的取值范围即可.
【解答】∵![]() 在实数范围内有意义,
在实数范围内有意义,
∴x-1≥0,
解得x≥1.
故答案为:x≥1.
【点评】本题考查的是二次根式有意义的条件,即被开方数大于等于0.
【答案】60°。
【考点】平行线的性质;三角形的外角性质.
【分析】利用三角形的一个外角等于与它不相邻的两个内角的和求出∠3的同位角的度数,再根据两直线平行,同位角相等即可求解.
【解答】如图,∵∠1=130°,∠2=70°,
∴∠4=∠1-∠2=130°-70°=60°,
∵a∥b,
∴∠3=∠4=60°.
故答案为:60°.
【点评】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,准确识图,理清图中各角度之间的关系是解题的关键.
【答案】![]() π.
π.
【考点】扇形面积的计算;三角形内角和定理.
【分析】根据三角形内角和定理得到∠B+∠C=180°-∠A=130°,利用半径相等得到OB=OD,OC=OE,则∠B=∠ODB,∠C=∠OEC,再根据三角形内角和定理得到∠BOD=180°-2∠B,∠COE=180°-2∠C,则∠BOD+∠COE=360°-2(∠B+∠C)=360°-2×130°=100°,图中阴影部分由两个扇形组成,它们的圆心角的和为100°,半径为3,然后根据扇形的面积公式计算即可.
【解答】∵∠A=50°,
∴∠B+∠C=180°-∠A=130°,
而OB=OD,OC=OE,
∴∠B=∠ODB,∠C=∠OEC,
∴∠BOD=180°-2∠B,∠COE=180°-2∠C,
∴∠BOD+∠COE=360°-2(∠B+∠C)
=360°-2×130°=100°,
而OB=![]() BC=3,
BC=3,
∴S阴影部分=![]() =
=![]() π.
π.
故答案为![]() π.
π.
【点评】本题考查了扇形面积的计算:扇形的面积=![]() (n为圆心角的度数,R为半径).也考查了三角形内角和定理.
(n为圆心角的度数,R为半径).也考查了三角形内角和定理.
计算:(答案用分数表示)
 ÷(-1);
÷(-1);
已知:如图,抛物线y=a(x-1)2+c与x轴交于点A(1-![]() ,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点
,0)和点B,将抛物线沿x轴向上翻折,顶点P落在点![]() (1,3)处.
(1,3)处.
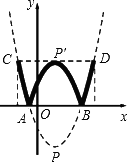
(1)求原抛物线的解析式;
(2)学校举行班徽设计比赛,九年级5班的小明在解答此题时顿生灵感:过点P'作x轴的平行线交抛物线于C、D两点,将翻折后得到的新图象在直线CD以上的部分去掉,设计成一个“W”型的班徽,“5”的拼音开头字母为W,“W”图案似大鹏展翅,寓意深远;而且小明通过计算惊奇的发现这个“W”图案的高与宽(CD)的比非常接近黄金分割比![]() (约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:
(约等于0.618).请你计算这个“W”图案的高与宽的比到底是多少?(参考数据:![]() ≈2.236,
≈2.236,![]() ≈2.449,结果可保留根号)
≈2.449,结果可保留根号)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com