答案：（1）∵四边形是正方形，∴，且   （2分）

又∵是公共边，∴△≌△，                              （2分）

∴∠ =∠                                                 （1分）

（2）联结                                                             （1分）

∵，

∴∠ =∠                                                 （1分）

∵∠=∠，∠ =∠，

∴∠=∠．

∵∠+∠=∠+∠，

∴∠=∠                                                   （1分）

∵四边形是正方形，

∴∠=∠ =45°，∠=∠= 45°，

∴∠=∠                                                  （1分）

∴∠=∠．                                                 （1分）

又∵∠是公共角，∴△∽△，                           （1分）

∴，即                                        （1分）

答案：（1）BD=CD……………1分

证△AEF≌△DEC

∴AF=CD

∵AF=BD

∴BD=CD……………5分

(2) 当△ABC满足：AB=AC时，四边形AFBD是矩形………6分

∵AF//BD, AF=BD

∴四边形AFBD是平行四边形

   ∵AB=AC，BD=CD

∴∠ADB=90°

∴□AFBD是矩形………10分

答案：(1)如图

(2)答：这条船继续前进，没有被浅滩阻碍的危险。

解：作CD⊥直线AB于点D，

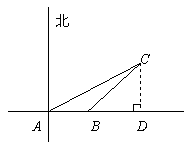         由已知可得∠CAD=30°, ∠CBD=45°，

         AB=100米。

         设CD=米。

         在Rt△ACD中

         tan∠CAD=

         ∴AD=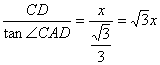

          在Rt△CBD中

         ∵∠CBD=45°, ∴BD=CD=x，

         ∵AD-BD=AB， ∴。

         解得

∴这条船继续前进没有被浅滩阻碍的危险。

答案：解：过D作DM⊥AE于M，过C作CN⊥AE于N，则：MN=CD=3米，设AM=x，则AN=x+3， 由题意：∠ADM =30^ｏ，∠ACN =45^ｏ，

在Rt△ADM中，DM=AM·cot30^ｏ=x，在Rt△ANC中，CN=AN=x+3，

又DM=CN=MB，∴x=x+3，解之得，x=（+1），∴AB=AM+MB=x+x+3=2×（+1）+3=3+6≈11（米）

【答案】x≥1。

【考点】二次根式有意义的条件．

【专题】存在型．

【分析】先根据二次根式有意义的条件列出关于x的不等式，求出x的取值范围即可．

【解答】∵在实数范围内有意义，

∴x－1≥0，

解得x≥1．

故答案为：x≥1．

【点评】本题考查的是二次根式有意义的条件，即被开方数大于等于0．