
题目列表(包括答案和解析)
已知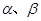 表示两个互相垂直的平面,
表示两个互相垂直的平面,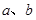 表示一对异面直线,则
表示一对异面直线,则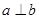 的一个充分条件是( )
的一个充分条件是( )
A.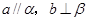 B.
B.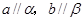
C.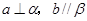 D.
D.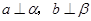
已知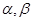 表示两个不同的平面,
表示两个不同的平面,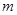 为平面
为平面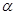 内的一条直线,则“
内的一条直线,则“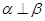 ”是“
”是“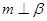 ”的( )
”的( )
A. 充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
已知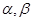 表示两个互相垂直的平面,
表示两个互相垂直的平面, 表示一对异面直线,则
表示一对异面直线,则
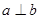 的一个充分条件是( )
的一个充分条件是( )
A.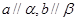 B.
B. 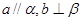 C.
C. 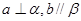 D .
D .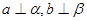
已知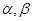 表示两个不同的平面,
表示两个不同的平面,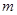 为
为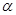 内一条直线,则“
内一条直线,则“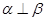 ”是“
”是“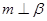 ”的( )
”的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
已知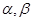 表示两个不同的平面,
表示两个不同的平面,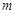 是一条直线且
是一条直线且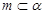 ,则“
,则“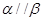 ”是“
”是“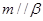 ”的
”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
一、选择题(每小题5分,共50分)
1.B 2.C 3.A 4.D 5.C 6.D 7.B 8.C 9.A 10.D
二、填空题(每小题4分,共24分)
11.180 12.60 13. 14.2 15.5 16.
14.2 15.5 16.
三、解答题(本大题共6小题,共76分)
17.(本题12分)
解:(Ⅰ)
 ………………………………(2分)
………………………………(2分)

 …………(4分)
…………(4分)

 …………………………………(6分)
…………………………………(6分)
(Ⅱ)
 . ……………(8分)
. ……………(8分)
由已知条件
根据正弦定理,得 …………………(10分)
…………………(10分)
 ……………………(12分)
……………………(12分)
18.(本题12分)
解:(Ⅰ) ……………………(2分)
……………………(2分)
 ……………………(4分)
……………………(4分)


 ……………………(6分)
……………………(6分)
当 时,有
时,有 (人).
(人).
 在
在 的基础上,
的基础上, 有
有 (人),
(人),
 ……………………(8分)
……………………(8分)
(Ⅱ) …………(10分)
…………(10分)

 …………………………………(12分)
…………………………………(12分)
19.(本题12分)
 证明:(Ⅰ)
证明:(Ⅰ) 在△
在△ 中,
中,





 …………………………(2分)
…………………………(2分)

 平面
平面 .
…………………………(4分)
.
…………………………(4分)
 平面
平面
 …………………………(6分)
…………………………(6分)
(Ⅱ)连接 交
交 于M,则M为
于M,则M为 的中点 …………………………(8分)
的中点 …………………………(8分)
连接DM,则 ∥
∥ ,
…………………………(10分)
,
…………………………(10分)
 平面
平面 ,
, 平面
平面 ,
,
 ∥平面
∥平面 …………………………(12分)
…………………………(12分)
20.(本题12分)
解:(Ⅰ)由已知得 ,又
,又 ,
,
 即
即 . …………………………(2分)
. …………………………(2分)
 ,公差
,公差 .
.
由 ,得 …………………………(4分)
,得 …………………………(4分)

即 .解得
.解得 或
或 (舍去).
(舍去).
 .
…………………………(6分)
.
…………………………(6分)
(Ⅱ)由 得
得
 …………………………(8分)
…………………………(8分)
 …………………………(9分)
…………………………(9分)
 是等差数列.
是等差数列.
则
 ………………………(11分)
………………………(11分)
 ……………………(12分)
……………………(12分)
21.(本题14分)
解:(Ⅰ)依题意得
 .
………………………(2分)
.
………………………(2分)
把(1,3)代入 .
.
解得 .
.
 椭圆的方程为
椭圆的方程为 .
………………………(4分)
.
………………………(4分)
(Ⅱ)由(Ⅰ)得 ,设
,设 ,如图所示
,如图所示

 点在椭圆上,
点在椭圆上,
 . ①
. ①
 点异于顶点
点异于顶点 、
、 ,
,
 .
.
由 、
、 、
、 三点共线,可得
三点共线,可得
从而 …………………………(7分)
…………………………(7分)
 ② …………(8分)
② …………(8分)
将①式代入②式化简得 …………(10分)
…………(10分)

 …………(12分)
…………(12分)
于是 为锐角,
为锐角, 为钝角. ……………(14分)
为钝角. ……………(14分)
22.(本题14分)
解:(Ⅰ) ,
,
令 ,得
,得 或
或 .
………………(2分)
.
………………(2分)
当 时,
时, 在
在 上单调递增;
上单调递增;
当 时,
时, 在
在 上单调递减,
上单调递减,
而 ,
,
 当
当 时,
时, 的值域是
的值域是 . ……………(4分)(Ⅱ)设函数
. ……………(4分)(Ⅱ)设函数 在
在 上的值域是A,
上的值域是A,
 若对任意
若对任意 .总存在
.总存在 1,使
1,使 ,
,
 .
……………(6分)
.
……………(6分)
 .
.
①当 时,
时, ,
,
 函数
函数 在
在 上单调递减.
上单调递减.
 ,
,
 当
当 时,不满足
时,不满足 ; ……………………(8分)
; ……………………(8分)
②当 时,
时, ,
,
令 ,得
,得 或
或 (舍去 ………………(9分)
(舍去 ………………(9分)
(i) 时,
时, 的变化如下表:
的变化如下表:

0



2

-
0
+

0




 .
.

 ,解得
,解得 . …………………(11分)
. …………………(11分)
(ii)当 时,
时,
 函数
函数 在
在 上单调递减.
上单调递减.

 ,
, 当
当 时,不满足
时,不满足 .
…………………(13分)
.
…………………(13分)
综上可知,实数 的取值范围是
的取值范围是 . ……………………(14分)
. ……………………(14分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com