
题目列表(包括答案和解析)
 (a为常数,且a>0)对于下列命题:
(a为常数,且a>0)对于下列命题:
 (a为常数,且a>0),对于下列命题:
(a为常数,且a>0),对于下列命题: ;
; )<
)< ;
; (a为常数,且a>0)对于下列命题:
(a为常数,且a>0)对于下列命题:
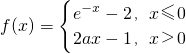 (a为常数,且a>0)对于下列命题:
(a为常数,且a>0)对于下列命题:
关于函数![]() (a为常数,且a>0)对于下列命题:
(a为常数,且a>0)对于下列命题:
①函数f(x)的最小值为-1; ②函数f(x)在每一点处都连续;
③函数f(x)在R上存在反函数; ④函数f(x)在x=0处可导;
⑤对任意的实数x1<0, x2<0且x1<x2,恒有![]() .
.
其中正确命题的序号是_____________.
1.B 2.B 3.C 4.C 5.B 6.D 7.A 8.C 9.D 10.A
11.31003 12.60 13..files\image154.gif) 14.
14..files\image156.gif) 15.①②⑤
15.①②⑤
16.解:(1)设“取出两个红球”为事件A,“取出一红一白两个球”为事件B,则
.files\image158.gif) ……2分
……2分
由题意得.files\image160.gif)
则有.files\image162.gif) ,可得
,可得.files\image164.gif) ……4分
……4分
∵.files\image166.gif) ,∴m为奇数……6分
,∴m为奇数……6分
(2)设“取出两个白球”为事件C,则.files\image168.gif) ……7分
……7分
由题意知.files\image170.gif) ,即有
,即有.files\image172.gif)
可得到.files\image174.gif) ,从而m+n为完全平方数……9分
,从而m+n为完全平方数……9分
又m≥n≥4及m+n≤20得9≤m+n≤20
得到方程组:.files\image176.gif) ;
;.files\image178.gif)
解得:.files\image180.gif) ,(不合题意舍去)
,(不合题意舍去).files\image182.gif) ……11分
……11分
故满足条件的数组(m, n)只有一组(10,6)……12分
17.解:(1)∵.files\image184.gif) ,……2分
,……2分
即.files\image186.gif)
即.files\image188.gif) ……4分
……4分
由于.files\image190.gif) ,故
,故.files\image192.gif) ……6分
……6分
(2)由.files\image194.gif) ……8分
……8分
.files\image196.gif) ……10分
……10分
.files\image198.gif)
当且仅当tanA=tanB,即A=B时,tanC取得最大值.files\image200.gif) .
.
所以C的最大值为.files\image202.gif) ,此时
,此时.files\image204.gif) 为等腰三角形. ……12分
为等腰三角形. ……12分
18.解:设裁员x人,可获得的经济效益为y万元,
则.files\image206.gif) ……4分
……4分
依题意.files\image208.gif)
又140<2a<420, 70<a<210. ……6分
(1)当.files\image210.gif) 时,x=a-70, y取到最大值;……8分
时,x=a-70, y取到最大值;……8分
(2)当.files\image212.gif) 时,
时,.files\image214.gif) , y取到最大值;……10分
, y取到最大值;……10分
答:当.files\image216.gif) 时,裁员a-70人;当
时,裁员a-70人;当.files\image218.gif) 时,裁员
时,裁员.files\image220.gif) 人……12分
人……12分
19.解法一:(1)作.files\image222.gif) ,垂足为O,连结AO,由侧面
,垂足为O,连结AO,由侧面.files\image224.gif) 底面ABCD,得
底面ABCD,得.files\image226.gif) 底面
底面.files\image228.jpg) ABCD. 因为SA=SB,所以AO=BO. 又
ABCD. 因为SA=SB,所以AO=BO. 又.files\image230.gif) ,故
,故.files\image232.gif) 为等腰直角三角形,
为等腰直角三角形,.files\image234.gif) 由三垂线定理,得
由三垂线定理,得.files\image236.gif)
(2)由(1)知.files\image238.gif) ,依题设
,依题设.files\image240.gif) ,故
,故.files\image242.gif) ,由
,由.files\image244.gif) ,得
,得.files\image246.gif) 所以
所以.files\image248.gif) 的面积
的面积.files\image250.gif) 连结DB,得
连结DB,得.files\image252.gif) 的面积
的面积.files\image254.gif) 设D到平面SAB的距离为h,由
设D到平面SAB的距离为h,由.files\image256.gif) ,
,
得.files\image258.gif) ,解得
,解得.files\image260.gif)
.files\image262.jpg) 设SD与平面SAB所成角为
设SD与平面SAB所成角为.files\image264.gif) ,则
,则.files\image266.gif) 所以直线SD与平面SAB所成的角为
所以直线SD与平面SAB所成的角为.files\image268.gif)
解法二:(1)作.files\image222.gif) ,垂足为O,连结AO,由侧面
,垂足为O,连结AO,由侧面.files\image224.gif) 底面ABCD,得
底面ABCD,得.files\image226.gif) 平面ABCD. 因为SA=SB,所以AO=BO. 又
平面ABCD. 因为SA=SB,所以AO=BO. 又.files\image230.gif) ,
,.files\image232.gif) 为等腰直角三角形,
为等腰直角三角形,.files\image234.gif)
如图,以O为坐标原点,OA为x轴正向,建立直角坐标系O―xyz,.files\image275.gif)
.files\image277.gif) ,所以
,所以.files\image236.gif)
(2)取AB中点E,.files\image280.gif) . 连结SE,取SE中点G,连结OG,
. 连结SE,取SE中点G,连结OG,.files\image282.gif)
.files\image284.gif) ,OG与平面SAB内两条相交直线SE、AB垂直,所以
,OG与平面SAB内两条相交直线SE、AB垂直,所以.files\image286.gif) 平面SAB.
平面SAB..files\image288.gif) 的夹角记为
的夹角记为.files\image264.gif) ,SD与平面SAB所成的角记为
,SD与平面SAB所成的角记为.files\image291.gif) ,则
,则.files\image264.gif) 与
与.files\image291.gif) 互余.
互余.
.files\image295.gif)
所以直线SD与平面SAB所成的角为.files\image268.gif)
20.解:(1)∵焦点F为(1,0),过点F且与抛物线交于点A、B的直线可设为.files\image298.gif) ,代入抛物线
,代入抛物线.files\image300.gif) 得:
得:.files\image302.gif) ,则有
,则有.files\image304.gif) ……2分
……2分
进而.files\image306.gif) ……4分
……4分
又.files\image308.gif) ,
,
得.files\image310.gif) 为钝角,故
为钝角,故.files\image232.gif) 不是直角三角形.……6分
不是直角三角形.……6分
(2)由题意得AB的方程为.files\image313.gif) ,
,
代入抛物线.files\image300.gif) ,求得
,求得.files\image316.gif) ……8分
……8分
假设抛物线上存在点.files\image318.gif) ,使
,使.files\image204.gif) 为直角三角形且C为直角,此时,以AC为直径的圆的方程为
为直角三角形且C为直角,此时,以AC为直径的圆的方程为.files\image321.gif) ,将A、B、C三点的坐标代入得:
,将A、B、C三点的坐标代入得:.files\image323.gif)
整理得:.files\image325.gif) ……10分
……10分
解得.files\image327.gif) 对应点B,
对应点B,.files\image329.gif) 对应点C……12分
对应点C……12分
则存在.files\image331.gif) 使
使.files\image204.gif) 为直角三角形.
为直角三角形.
故满足条件的点C有一个:.files\image331.gif) ……13分
……13分
.files\image335.jpg)
∴.files\image337.gif)
令.files\image339.gif)
由.files\image341.gif)
∴当.files\image343.gif) 时,h(t)单调递增,∴h(t)>h(1)=0
时,h(t)单调递增,∴h(t)>h(1)=0
于是.files\image345.gif) ……②
……②
由①、②可知.files\image347.gif) ……10分
……10分
所以,.files\image349.gif) ,即
,即.files\image351.gif) ……11分
……11分
(3)由(2)可知.files\image353.gif)
在.files\image349.gif) 中令n=1, 2, 3, …, 2007,并将各式相加得
中令n=1, 2, 3, …, 2007,并将各式相加得
.files\image356.gif)
即.files\image358.gif) ……14分
……14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com