
题目列表(包括答案和解析)
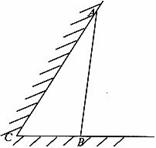
如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即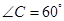 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记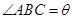 ,
,
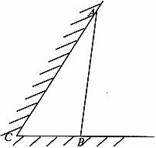
(1)问当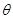 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
(2)若饲养场建造成扇形,养殖场的面积能比(1)中的最大面积更大?说明理由。
如图所示,某饲养场要建造一间两面靠墙的三角形露天养殖场,已知已有两面墙的夹角为60°(即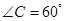 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记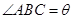 ,
,
(1)问当 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?
(2)若饲养场建造成扇形,养殖场的面积能比(1)中的最大面积更大?说明理由。
 ),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记
),现有可供建造第三面围墙的材料60米(两面墙的长均大于60米),为了使得小老虎能健康成长,要求所建造的三角形露天活动室尽可能大,记 ,
,
 为多少时,所建造的三角形露天活动室的面积最大?
为多少时,所建造的三角形露天活动室的面积最大?在数列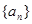 中,
中,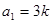 ,其中
,其中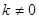 ,对任意
,对任意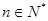 都有:
都有: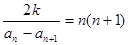 ;(1)求数列
;(1)求数列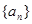 的第2项和第3项;
的第2项和第3项;
(2)求数列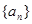 的通项公式
的通项公式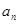 ,假设
,假设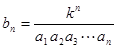 ,试求数列
,试求数列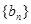 的前
的前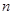 项和
项和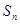 ;
;
(3)若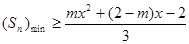 对一切
对一切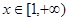 恒成立,求
恒成立,求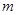 的取值范围。
的取值范围。
【解析】第一问中利用)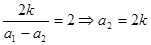 同理得到
同理得到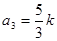
第二问中,由题意得到: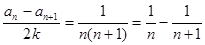
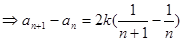
累加法得到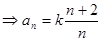
第三问中,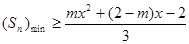 利用恒成立,转化为最小值大于等于即可。得到范围。
利用恒成立,转化为最小值大于等于即可。得到范围。
(1)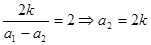 同理得到
同理得到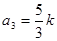 ……2分
……2分
(2)由题意得到: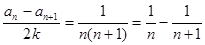
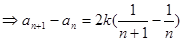
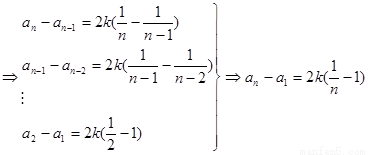 又
又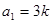
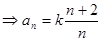 ……5分
……5分
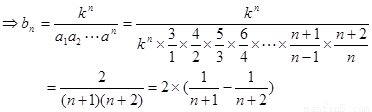
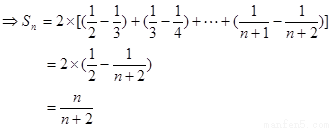 ……8分
……8分
(3)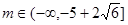
一支车队有15辆车,某天依次出发执行运输任务,第一辆车于下午2时出发,第二辆车于下午2时10分出发,第三辆车于下午2时20分出发,依此类推。假设所有的司机都连续开车,并都在下午6时停下来休息。
(1)到下午6时最后一辆车行驶了多长时间?
(2)如果每辆车的行驶速度都是60 ,这个车队当天一共行驶了多少千米?
,这个车队当天一共行驶了多少千米?
【解析】第一问中,利用第一辆车出发时间为下午2时,每隔10分钟即 小时出发一辆
小时出发一辆
则第15辆车在 小时,最后一辆车出发时间为:
小时,最后一辆车出发时间为: 小时
小时
第15辆车行驶时间为: 小时(1时40分)
小时(1时40分)
第二问中,设每辆车行驶的时间为: ,由题意得到
,由题意得到
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
则行驶的总时间为:
则行驶的总里程为: 运用等差数列求和得到。
运用等差数列求和得到。
解:(1)第一辆车出发时间为下午2时,每隔10分钟即 小时出发一辆
小时出发一辆
则第15辆车在 小时,最后一辆车出发时间为:
小时,最后一辆车出发时间为: 小时
小时
第15辆车行驶时间为: 小时(1时40分)
……5分
小时(1时40分)
……5分
(2)设每辆车行驶的时间为: ,由题意得到
,由题意得到
 是以
是以 为首项,
为首项, 为公差的等差数列
为公差的等差数列
则行驶的总时间为: ……10分
……10分
则行驶的总里程为:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com