
题目列表(包括答案和解析)
根据不等式的基本性质,把下列不等变为x>a或x<a的形式:
(1)![]() >-3;
>-3;
(2)-2x<6.
解::(1)不等式的两边都乘以2,不等式的方向不变,所以![]() ,得x>-6.
,得x>-6.
(2)不等式两边都除以-2,不等式方向改变,所以![]() ,得x>-3.
,得x>-3.
上面两小题中不等式的变形与方程的什么变形相类似?有什么不同的?
一、阅读理解:
在△ABC中,BC=a,CA=b,AB=c;
(1)若∠C为直角,则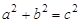 ;
;
(2)若∠C为为锐角,则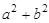 与
与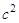 的关系为:
的关系为: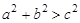
证明:如图过A作AD⊥BC于D,则BD=BC-CD=a-CD
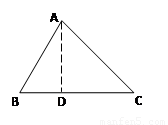
在△ABD中:AD2=AB2-BD2
在△ACD中:AD2=AC2-CD2
AB2-BD2= AC2-CD2
c2-(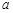 -CD)2= b2-CD2
-CD)2= b2-CD2
∴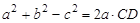
∵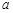 >0,CD>0
>0,CD>0
∴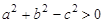 ,所以:
,所以: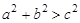
(3)若∠C为钝角,试推导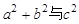 的关系.
的关系.
二、探究问题:在△ABC中,BC=a=3,CA=b=4,AB=c;若△ABC是钝角三角形,求第三边c的取值范围.
知识背景:同学们已经学过有理数的大小比较,那么两个代数式如何比较大小呢?我们通常用作差法比较代数式大小。例如:已知M=2x+3,N=2x+1,比较M和N的大小。先求M-N,若M-N>0,则M>N;若M-N<0,则M<N;若M-N=0,则M=N,本题中因为M-N=2>0,所以M>N。
知识应用:图⑴是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图⑵所示的新长方形,此长方形的面积为 ;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
;将图(1)中正方形边长增加2得到如图⑶所示的新正方形,此正方形的面积为
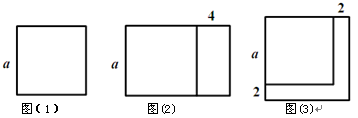
①用含a的代数式表示 ,
,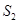 (需要化简)
(需要化简)
②请你用作差法比较 与
与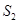 大小
大小
阅读材料:已知p2-p-1=0 , 1-q-q2=0
, 且pq≠1 ,求 的值.
的值.
解:由p2-p-1=0及1-q-q2=0,可知p≠0,q≠0,
又因为pq≠1 所以p≠ ,所以1-q-q2 =0可变形为:(
,所以1-q-q2 =0可变形为:( )2-(
)2-( )-1=0 ,
)-1=0 ,
根据p2-p-1=0和( )2-(
)2-( )-1=0的特征,
)-1=0的特征,
p与 可以看作方程x2-x-1=0的两个不相等的实数根,所以p+
可以看作方程x2-x-1=0的两个不相等的实数根,所以p+ =1, 所以
=1, 所以 =1.
=1.
根据以上阅读材料所提供的方法,完成下面的解答:
1.已知m2-5mn+6n2=0,m>n,求 的值
的值
2.已知2m2-5m-1=0,( )2+
)2+ -2=0,且m≠n ,求
-2=0,且m≠n ,求 的值.
的值.
如图,等腰直角三角形ABC中,AC=BC>3,点M在AC上,点N在CB的延长线上,MN交AB于点O,且AM=BN=3,则S△AMO与S△BNO的差是( ▲ )

A.9 B.4.5 C.0 D.因为AC、BC的长度未知,所以无法确定
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com