
题目列表(包括答案和解析)
(本小题满分14分)
已知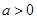 ,函数
,函数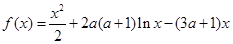 。
。
(1)若函数 在
在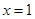 处的切线与直线
处的切线与直线 平行,求
平行,求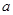 的值;
的值;
(2)讨论函数 的单调性;
的单调性;
(3)在(1)的条件下,若对任意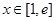 ,
,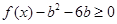 恒成立,求实数
恒成立,求实数 的取值组成的集合。
的取值组成的集合。
(本小题满分14分)
已知 为函数
为函数 图象上一点,
图象上一点, 为坐标原点.记直线
为坐标原点.记直线 的斜率
的斜率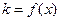 。
。
(I)同学 甲发现:点
甲发现:点 从左向右运动时,
从左向右运动时, 不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断。
不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断。
(Ⅱ)求证:当 时,
时, 。
。
(III)同学乙发现:总存在正实数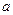 、
、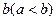 ,使
,使 .试问:他的判断是否正确?若不正确,请说
.试问:他的判断是否正确?若不正确,请说 明理由:若正确,请求出
明理由:若正确,请求出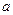 的取值范围。
的取值范围。
(本小题满分14分)
已知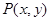 为函数
为函数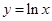 图象上一点,
图象上一点,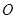 为坐标原点.记直线
为坐标原点.记直线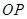 的斜率
的斜率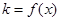 。
。
(I)同学甲发现:点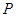 从左向右运动时,
从左向右运动时,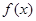 不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断。
不断增大,试问:他的判断是否正确?若正确,请说明理由:若不正确,请给出你的判断。
(Ⅱ)求证:当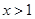 时,
时,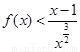 。
。
(III)同学乙发现:总存在正实数 、
、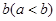 ,使
,使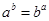 .试问:他的判断是否正确?若不正确,请说明理由:若正确,请求出
.试问:他的判断是否正确?若不正确,请说明理由:若正确,请求出 的取值范围。
的取值范围。
(本小题满分14分) 已知:函数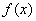 的定义域为
的定义域为 ,且满足对于任意
,且满足对于任意 ,都有
,都有 ,
,
(1)求: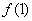 的值; (2)判断
的值; (2)判断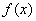 的奇偶性并证明;
的奇偶性并证明;
(3)如果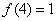 ,
, 且
且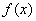 在
在 上是增函数,求:
上是增函数,求: 的取值范围。
的取值范围。
(本小题满分14分)
已知幂函数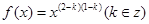 在定义域上递增。
在定义域上递增。
(1)求实数k的值,并写出相应的函数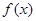 的解析式;
的解析式;
(2)对于(1)中的函数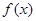 ,试判断是否存在正数m,使函数
,试判断是否存在正数m,使函数
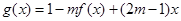 ,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
,在区间上的最大值为5。若存在,求出m的值;若不存在,请说明理由。
一、ADBAB CDCBC
二、11 9 12  13 384 14
13 384 14  15
15 

三、解答题
16.解:(I)
又 ,∴
,∴ ,
, ……5分
……5分
(II)

17.解:(Ⅰ) 抛掷一次出现的点数共有6×6 = 36种不同结果,其中“点数之和为
∴抛掷一次出现的点数之和为7的概率为 ………………………… 2分
………………………… 2分
ξ可取1 , 2 , 3 , 4
P (ξ=1) = ,P (ξ=2) =
,P (ξ=2) = ,P (ξ= 3) =
,P (ξ= 3) =
P (ξ= 4) =
∴ξ的概率分布列为
ξ
1
2
3
4
P



|