
题目列表(包括答案和解析)
() (本小题满分13分)
在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是![]() ,
,![]() .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
(Ⅰ)求3次投篮的人依次是甲、甲、乙的概率;
(Ⅱ)若投篮命中一次得1分,否则得0分. 用ξ表示甲的总得分,求ξ的分布列和数学期望.
(本小题满分13分)
在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是![]() ,
,![]() .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
(Ⅰ)求3次投篮的人依次是甲、甲、乙的概率;
(Ⅱ)若投篮命中一次得1分,否则得0分. 用ξ表示甲的总得分,求ξ的分布列和数学期望.
(本小题满分13分)
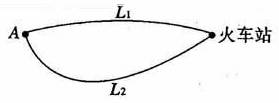
如图,A地到火车站共有两条路径L1和L2,据统计,通过两条路径所用的时间互不影响,所用时间落在各时间段内的频率如下表:
| 时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| L1的频率 | 0.1 | 0.2 | 0.3 | 0.2 | 0.2 |
| L2的频率 | 0 | 0.1 | 0.4 | 0.4 | 0.1 |
现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站。
(Ⅰ)为了尽最大可能在各自允许的时间内赶到火车站,甲和乙应如何选择各自的路径?
 (Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望。
(Ⅱ)用X表示甲、乙两人中在允许的时间内能赶到火车站的人数,针对(Ⅰ)的选择方案,求X的分布列和数学期望。
(本小题满分13分)
在某校组织的一次篮球定点投篮比赛中,两人一对一比赛规则如下:若某人某次投篮命中,则由他继续投篮,否则由对方接替投篮. 现由甲、乙两人进行一对一投篮比赛,甲和乙每次投篮命中的概率分别是![]() ,
,![]() .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
(Ⅰ)求3次投篮的人依次是甲、甲、乙的概率;
(Ⅱ)若投篮命中一次得1分,否则得0分. 用ξ表示甲的总得分,求ξ的分布列和数学期望.
 ,
,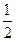 .两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
.两人共投篮3次,且第一次由甲开始投篮. 假设每人每次投篮命中与否均互不影响.
一、选择题:本大题共12小题,每小题5分,共60分。
1―5 DBCDC 6―10BBCAB 11―12 DB
二、填空题:本大题共4小题,每小题4分,共16分。
13.“ ” 14.
” 14. 15.1200 16.
15.1200 16.
三、解答题:本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分13分)
解:(I)由已知

(II)

|