
题目列表(包括答案和解析)
平面内与两定点 、
、
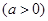 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上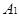 、
、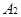 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
平面内与两定点 、
、
 连线的斜率之积等于非零常数
连线的斜率之积等于非零常数 的点的轨迹,加上
的点的轨迹,加上 、
、 两点所成的曲线
两点所成的曲线 可以是圆、椭圆或双曲线。求曲线
可以是圆、椭圆或双曲线。求曲线 的方程,并讨论
的方程,并讨论 的形状与
的形状与 值的关系。
值的关系。
【解析】本试题主要考查了平面中动点的轨迹方程,利用斜率之积为定值可以对参数进行分类讨论,并得到关于不同曲线的参数的范围问题。对于方程的特点做了很好的考查和运用。
已知动点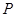 与平面上两定点
与平面上两定点 连线的斜率的积为定值
连线的斜率的积为定值 .
.
(1)试求动点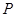 的轨迹方程
的轨迹方程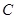 ;
;
(2)设直线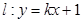 与曲线
与曲线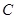 交于M.N两点,当
交于M.N两点,当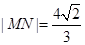 时,求直线
时,求直线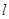 的方程.
的方程.
【解析】本试题主要是考查了轨迹方程的求解以及直线与椭圆位置关系的运用。
已知动点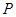 与平面上两定点
与平面上两定点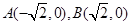 连线的斜率的积为定值
连线的斜率的积为定值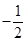 .
.
(1)试求动点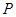 的轨迹方程
的轨迹方程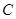 ;
;
(2)设直线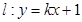 与曲线
与曲线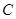 交于M.N两点,当
交于M.N两点,当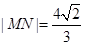 时,求直线
时,求直线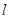 的方程.
的方程.
【解析】本试题主要是考查了轨迹方程的求解以及直线与椭圆位置关系的运用。
已知动点 与平面上两定点
与平面上两定点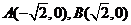 连线的斜率的积为定值
连线的斜率的积为定值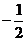 .
.
(1)试求动点 的轨迹方程
的轨迹方程 ;
;
(2)设直线 与曲线
与曲线 交于M.N两点,当
交于M.N两点,当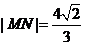 时,求直线
时,求直线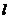 的方程.
的方程.
【解析】本试题主要是考查了轨迹方程的求解以及直线与椭圆位置关系的运用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com